大眼金枪鱼(Thunnus obesus)是热带东太平洋最主要的商业性金枪鱼鱼种，由区域性渔业管理组织——美洲间热带金枪鱼委员会(IATTC)负责管理。作为渔业管理的重要科学依据，其资源评估却存在很大的不确定性(Uncertainty)，尽管最近的评估认为其资源状态已有所恢复，亲体量略高于最大持续产量相应的水平(Aires-da-Silva et al, 2015)。种群结构、生物学参数、亲体-补充量关系、资源评估模型类型、模型结构假设等均会影响模型的参数估算，从而影响生物学参考点的估算和资源状态的判断(Aires-da-Silva et al, 2014)。生物学参考点是从生物学的角度描述或衡量资源开发状态的指标，常以资源生物量和捕捞死亡系数来表示。在渔业资源评估实践中，考虑不确定性是不可或缺的重要环节(Patterson et al, 2001)。一般将不确定性分为4类误差：测量误差、过程误差、模型误差和操作误差(Chen et al, 1998)。尽管4类误差常共存于一个渔业系统，为了简化研究，模型误差和操作误差通常不予考虑，在东太平洋大眼金枪鱼的历年评估中也是如此。

近10多年来，东太平洋金枪鱼类资源评估采用的主要模型有A-SCALA (Maunder et al, 2003)和Stock Synthesis 3 (SS3)(Methot et al, 2013)。A-SCALA是在Multifan-CL模型(中西太平洋金枪鱼类资源评估的主要模型)(Fournier et al, 1998)基础上创建的年龄结构模型。SS3于2007年开始被用于东太平洋大眼金枪鱼资源评估。SS3可以构建从简单的年龄结构生物量动态模型，到复杂的统计年龄结构模型(Methot et al, 2013)，可以利用渔获量、资源(相对)丰度指数、渔获年龄结构组成和体长结构组成、标志放流数据等渔业资源调查和监测中获得的各项数据，能估算常用的渔业管理生物学参考点，并且能模拟各种捕捞策略对资源进行“管理”。此外，还可以用作操作模型(Operating model)进行计算机渔业模拟研究，实际上，SS3可认为是一个资源评估的模型平台，而非单一的模型。由于包含的功能较多，SS3已成为运用最广泛的综合性资源评估模型之一，尤其在北美(Methot et al, 2013)，也逐渐被三大洋的金枪鱼渔业区域性管理组织接受(除中西部太平洋之外)，成为其开展资源评估的主要模型。由于对渔业数据的要求较高，目前，SS3模型尚未在我国近海的鱼类资源评估中运用。

东太平洋大眼金枪鱼渔业结构复杂，主要作业类型为围网和延绳钓，围网分为主捕自由鱼群和人工集鱼群的不同方式。不同类型的作业区域、历史时期和捕捞效率不同(Aires-da-Silva et al, 2014)，近期大眼金枪鱼的SS3模型实际为“基于体长组成的统计年龄结构模型”(Length-based, statistical age-structured model)，本研究称为复杂模型(Full model)，共含23种渔业，模型结构庞大、参数多、解释复杂。对模型结构进行简化，将有助于提高资源评估工作的效率。虽然当前资源评估模型和方法的发展趋于复杂化，但研究者们仍致力于简单模型和方法的开发(Cotter et al, 2004; Jardim et al, 2015)。

近期，研究者尝试为大眼金枪鱼构建较为简单的SS3模型，但该类模型目前仅是用于模拟研究中的操作模型(Wang et al, 2014; Zhu et al, 2016)，能否用于评估实际的大眼金枪鱼资源，尚未有相应的研究。本研究尝试对东太平洋大眼金枪鱼SS3模型进行简化，通过对简化模型(Simplified model)的效果评价，考察简化模型对该资源的评估能力。由于真实的资源动态我们无法获知，为了简便，本研究假设复杂模型描述的资源动态最接近于“真实”情况，从而将简化模型的结果与复杂模型的结果进行比较，作为评价依据。

生物学参数的设置与近期的资源评估基本一致(Aires-da-Silva et al, 2014)，均假设为已知常数。假设东太平洋大眼金枪鱼为一个资源群体，群体内的个体处于完全、随机的混合状态(Maunder et al, 2006)。年龄与生长采用von Bertalanffy生长模型，但考虑幼鱼和成鱼具有不同的生长变异，即相同年龄的体长不同，大眼金枪鱼共分为40个“季龄组”，即最高年龄组为10龄组(为附加年龄组)。在SS3中，生长模型采用最小年龄和最大年龄(叉长分别为20.5 cm和185.5 cm，生长变异标准差分别为1.82 cm和12.04 cm)进行参数化，生长参数K=0.068/年。自然死亡率系数(M)考虑幼鱼和成鱼、雌性和雄性的差异。

统计年龄结构模型所需的基本渔业数据包括每种渔业的渔获量(Catch)、代表性渔业的渔获年龄组成或体长组成(Age/size composition)、代表性渔业的相对资源丰度指数(Relative abundance index)。本研究复杂模型的渔业数据结构与近期的实际评估基本相同，包含23种渔业(表 1)，其中，涉及围网的为渔业1-11，涉及延绳钓的为渔业12-23。评估模型中的渔业一般根据资料来源和捕捞选择性(Selectivity)来定义，与生产中的实际渔业类型有所区别。

表 1(Tab. 1)

表 1 东太平洋大眼金枪鱼SS3复杂模型对渔业的划分 Table 1 Fishery definition of full SS3 model for big-eye tuna in eastern Pacific Ocean 渔业Fishery 渔具Gear 年份Year 渔获数据特点Feature of the fishery data 1 PS(OBJ) 1975-1992 渔获量Catch 2 PS(OBJ) 1993-2012 渔获量+丢弃量(渔业2-5的体长组成采样区域不同)Catch+Discards(size data for fishery 2-5 obtained from different sampling area) 3 PS(OBJ) 1993-2012 4 PS(OBJ) 1993-2012 5 PS(OBJ) 1993-2012 6 PS(NOA, DEL), LP 1975-1989 渔获量Catch 7 PS(NOA, DEL), LP 1990-2012 渔获量+丢弃量Catch + Discards 8 PS(OBJ) 1993-2012 渔业2中丢弃的小个体Discards of small fish from fishery 2 9 PS(OBJ) 1993-2012 渔业3中丢弃的小个体Discards of small fish from fishery 3 10 PS(OBJ) 1993-2012 渔业4中丢弃的小个体Discards of small fish from fishery 4 11 PS(OBJ) 1993-2012 渔业5中丢弃的小个体Discards of small fish from fishery 5 12 LL 1975-1989 渔获尾数Catch in number, 10°N以北North of 10°N 13 LL 1990-2012 14 LL 1975-1989 渔获尾数0°-10°N之间Catch in number, Between 0° and 10°N 15 LL 1990-2012 16 LL 1975-1989 渔获尾数0°以南100°W以西Catch in number, South of 0°, West of 100°W 17 LL 1990-2012 18 LL 1975-1989 渔获尾数0°以南100°W以东Catch in number, South of 0°, East of 100°W 19 LL 1990-2012 20 LL 1990-2012 渔获量10°N以北Catch, North of 10°N 21 LL 1990-2012 渔获量0°-10°N之间Catch, Between 0° and 10°N 22 LL 1990-2012 渔获量0°以南100°W以西Catch, South of 0°, West of 100°W 23 LL 1990-2012 渔获量0°以南100°W以东Catch, South of 0°, East of 100°W 注：PS：围网；LP：竿钓；LL：延绳钓；OBJ：捕人工集鱼群的围网；NOA：捕自由鱼群的围网；DEL：捕海豚群的围网，修改自Aires-da-Silva等(2014) Note: PS: Purse seine; LP: Pole and line; LL: Longline; OBJ: Sets on floating objects; NOA: Sets on unassociated fish; DEL: Sets on dolphin schools, revised from Aires-da-Silva et al (2014)

表 1 东太平洋大眼金枪鱼SS3复杂模型对渔业的划分 Table 1 Fishery definition of full SS3 model for big-eye tuna in eastern Pacific Ocean

渔业数据时间跨度为1975年1月-2012年12月(2014年度评估的数据)，模型中以季度为种群动态变化的时间单位(共148个季节)。由于本研究的目的是比较复杂模型和简化模型的评估差异，而非评估其最近资源状况(该工作由IATTC秘书处在相应的公约框架下开展)，因此，未采用最新统计资料。资源丰度指数和体长组成资料来自主要的围网渔业(即人工集鱼作业)和延绳钓渔业(表 2)。

表 2(Tab. 2)

表 2 大眼金枪鱼复杂模型和简化模型采用的资料和渔业选择性曲线 Table 2 Fishery data and selectivity curve used in the full model and simplified model for big-eye tuna 复杂模型Full model 简化模型Simplified model 渔业Fishery 渔获量Catch 丰度指数Abundance index 体长组成Size composition 选择性Selectivity 渔业Fishery 渔获量Catch 丰度指数Abundance index 体长组成Size composition 选择性Selectivity 1 ○ ○ ○ B 围网Purse seine ● ● B 2 ○ ○ ○ B ● ● ● 3 ○ ○ ○ B ● ● 4 ○ ○ ○ B ● ● 5 ○ ○ ○ B ● ● 6 ○ ○ B ● 7 ○ ○ B ● 8 ○ 1 ● 9 ○ 1 ● 10 ○ 1 ● 11 ○ 1 ● 12 ○ ○ ○ B 延绳钓Longline ● A 13 ○ ○ ○ B ● 14 ○ ○ ○ B ● 15 ○ ○ ○ A ● 16 ○ ○ ○ B ● ● ● 17 ○ ○ ○ A ● ● ● 18 ○ ○ ○ B ● 19 ○ ○ ○ B ● 20 ○ B ● 21 ○ B ● 22 ○ B ● 23 ○ B ● 注：A：逻辑斯谛曲线；B：钟形曲线；1表示选择性=1；○、●分别表示复杂模型、简化模型利用了该项数据 Note: A: Logistic curve; B: Dome-shaped curve; 1 indicated selectivity=1; ○ and ● indicated the data were used in the full model and simplified model, respectively

表 2 大眼金枪鱼复杂模型和简化模型采用的资料和渔业选择性曲线 Table 2 Fishery data and selectivity curve used in the full model and simplified model for big-eye tuna

大眼金枪鱼复杂模型基于SS3平台(Methot et al, 2013)构建。该模型平台初建于20世纪80年代，起初用于底层鱼类资源评估，在用AD Model Builder (Fournier et al, 2012)重新编程后，改进了模拟拟合的效率。SS3模型平台分为3个子模型：种群动态模型，描述在生物学(生长、死亡、补充)和渔业共同作用下的资源变化；观测模型，描述渔业系统中不可观测变量与可观测变量的关系(如丰度指数与资源量关系)；统计模型，描述模型预测值与观测值之间的误差结构，并通过极大似然法估算模型参数。此外，还有预测模块，根据参数值计算生物学参考点，并可模拟预测不同管理措施下的资源变化。由于SS3模型结构庞大，本研究仅对与大眼金枪鱼评估所采用的主要模型结构作简单描述，更多技术细节可参见Methot (2000)和Methot等(2013)。

假设初始资源为平衡状态，则初始年(使用“年”为方便描述，实际为季节)性别为γ的a龄鱼资源量可表示为：

其中，${{N}_{\gamma ,A}}=\sum\limits_{a=A}^{3A-1}{{{N}_{\gamma ,a}}}+\frac{{{N}_{\gamma ,3A-1}}{{e}^{-a{{M}_{\gamma ,a}}}}}{1-{{e}^{-}}^{{{M}_{\gamma ,a}}}}\ \ \ \ a=A$

式中，c为补充群体的性比，M为自然死亡系数，A为附加年龄组，将资源量从0龄估算到3A-1龄的目的是平衡初始年龄结构，这是SS3模型的特殊之处。R₀为原始平衡状态的补充量。

在水温适合时，成熟的雌性大眼金枪鱼几乎终年均可产卵(Schaefer et al, 2005)，因此，模型里假设每年补充1次。初始年之后的补充量(0龄鱼的资源尾数，R)由前一年的亲体量(产卵群体生物量，SSB)、根据亲体-补充量关系模型决定：

式中，SSB₀是与R₀对应的亲体量，SSB_y为y年的亲体量，h为陡度参数。b_yσ_R为补充量变化修正项，为补充量对数转换后相对于各年平均值的标准差(假设为0.6)，$R_y^\% $ 为由此得到的正态分布误差结构。补充量变化修正的目的是使平均补充量为无偏估计(Methot et al, 2011)。初始年之后的资源量动态为：

式中，Z_{y, γ, a}为y年的性别γ、年龄组a的总死亡系数，F_{y, f}为渔业f的选择性S=1 (即“完全选择”)时的捕捞死亡系数。大眼金枪鱼SS3模型的F估算采用混合算法(Hybrid method)，即设定初始年的F为自由参数，根据渔获量方程(假设渔获量无误差)，通过反复迭代算法获得其他年份的F估计。捕捞死亡系数与体长结构的选择性的乘积、经体长-年龄转换，得到各年龄组的捕捞死亡系数。在23种渔业中，除渔业15、17为逻辑斯谛选择性曲线、渔业8-11为完全选择外，其他渔业的选择性均假设为钟形曲线(表 2)。

种群的许多变量(如绝对资源量)一般不能直接观测，观测模型的作用是将不可观测变量与可观测变量建立起联系。大眼金枪鱼的可观测变量是丰度指数和体长组成，相应的观测模型为：

式中，Q_f为渔业f的可捕系数，B_{y, f}为可捕资源量，I为丰度指数预测值。l_{1, γ}为最小体长组(Length bin)的下界，l_{2, γ}为最大体长组的上界，p_{y, f, γ, l}为体长组l的渔获(尾数)比例。

具有丰度指数观测资料的渔业，其相应的对数正态分布似然函数(Lognormal likelihood)可表示为：

式中，N为观测值个数，I为丰度指数观测值(即围网和延绳钓渔业CPUE)，σ为CPUE对数化后的(正态分布)误差结构的标准差(衡量丰度指数观测误差离散程度的指标，σ越小，表明丰度指数数据对模型参数估算的贡献越大)。根据以往的研究，围网和延绳钓的σ分别设为0.40和0.15。

具有体长组成观测资料的渔业，其相应的多项分布似然函数(Multinomial likelihood)可表示为：

式中，n是估算体长组成数据的有效年样本量(衡量取样精度的间接指标，n越大，表明体长组成数据越可信，对模型参数估算的贡献越大)，p为渔获比例观测值，$\hat{p}$ 为渔获比例的模型预测值。此外，SS3模型将补充量估算值(自由参数)与由亲体-补充量模型预测的补充量，建立对数正态分布的似然函数，与丰度指数和体长组成数据的似然函数式(7)、(8) 一起，构成总的参数估算目标函数。

SS3模型采用极大似然估算法进行参数估算，大眼金枪鱼复杂模型估算的参数包括初始补充量、补充量变化时间序列，每种渔业的捕捞死亡系数初始值、选择性曲线参数、可捕系数等。完成参数估算后，模型计算资源量、捕捞死亡系数等时间序列，接着运行预测模块，通过最优化算法求得最大持续产量和相应的捕捞死亡系数、亲体量等生物学参考点。

模型简化的方式有多种，如将年龄结构模型简化为生物量动态模型，或调整模型的参数化方法。本研究考虑保持SS3年龄结构模型的基本结构不变，即采用与复杂模型相同的种群动态模型、观测模型和统计模型及其误差结构，以及生物学假设和模型的参数化方法，唯一简化的是模型的渔业数据结构，以利于复杂模型和简化模型的结果比较。

考虑到捕捞大眼金枪鱼的基本渔具为围网和延绳钓(表 1)，因此，本研究将复杂模型的渔业数据结构简化为“围网”和“延绳钓”2种渔业，即将包含23种渔业的复杂模型简化为只有2种渔业的SS3年龄结构模型。简化的具体方法：对于渔获量，将原渔业1-11和原渔业12-23分别求和，作为简化模型的围网和延绳钓渔业的渔获量；对于资源丰度指数，采用东太平洋具有代表性的人工集鱼围网(原渔业2) 和延绳钓渔业(原渔业16-17) 的丰度指数(表 1)，作为简化模型中的围网渔业和延绳钓渔业的丰度指数；对于体长组成数据，选择人工集鱼围网(原渔业1-5) 和延绳钓渔业(原渔业16-17) 的体长组成，然后根据渔获量进行加权平均，作为简化模型的围网和延绳钓渔业的体长组成数据。渔业结构简化后，渔业选择性也要相应的调整，为此，假设围网渔业的选择性模型符合钟形曲线，延绳钓渔业的选择性模型为逻辑斯谛曲线(表 2)，其参数化方法与复杂模型相同。

为了评价简化模型的评估效果，采用7个关键生物学参考点和资源状态变量进行比较，包括MSY(最大持续产量)、F_MSY(资源处在产出MSY时的捕捞死亡系数)、F_multiplier(以MSY为管理目标时，当前捕捞死亡系数应调整的比例)、SSB_MSY/SSB₀(资源处在产出MSY时的SSB与原始种群的SSB之比)、C_curr/MSY(当前渔获量与MSY之比)、F_curr/F_MSY(当前捕捞死亡系数与产出MSY时的捕捞死亡系数之比)、SSB_curr/SSB_MSY(当前SSB与MSY时的SSB之比)。其中，SSB_MSY/SSB₀反映了捕捞引起的亲体量下降水平，F_curr/F_MSY和SSB_curr/SSB_MSY是目前金枪鱼资源评估中判断资源过度捕捞状态的2个主要参考点。

由于资源评估模型的关键假设参数会影响结果，对于大眼金枪鱼近期的研究表明(Aires-da-Silva et al, 2014)，自然死亡系数和陡度是影响结果的最重要参数。因此，本研究针对这2个参数做不确定性分析(即敏感性分析)，对复杂模型和简化模型的自然死亡系数和陡度参数均考虑3个不同水平，自然死亡系数见图 1。从图 1可以看出，陡度h的3个水平分别为1.0、0.9、0.8。不同M水平的模型(F4-F6，S4-S6)，其h均假设为1.0；不同h水平的模型(F1-F3，S1-S3)，其M均假设在较高水平。共得到12个具体的模型(表 3)。

图 1(Fig. 1)

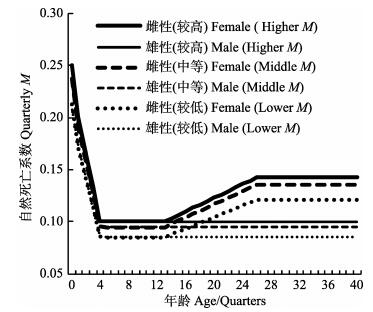
图 1 大眼金枪鱼自然死亡系数的3个水平 Figure 1 Three levels of natural mortality of big-eye tuna

表 3(Tab. 3)

表 3 大眼金枪鱼SS3模型参数个数及拟合时间比较 Table 3 Comparison of numbers of parameters and the fitting time of SS3 model for big-eye tuna 模型Model 假设Assumption 参数个数Number of parameters 拟合时间Fit time (min)* 原始补充量(千尾) R0 (Thousand fish) 原始亲体量SSB0 (t) 模型编号Model code 复杂模型Full model 陡度h=1.0 234 48 5826 296905 F1 陡度h=0.9 234 47 6418 327116 F2 陡度h=0.8 234 45 7274 370705 F3 简化模型Simplified model 陡度h=1.0 176 27 6498 331161 S1 陡度h=0.9 176 8 7295 371774 S2 陡度h=0.8 176 12 8351 425615 S3 复杂模型Full model 较高M Higher M 234 50 5826 296905 F4 中等M Middle M 234 68 5336 317009 F5 较低M Lower M 234 88 4377 357304 F6 简化模型Simplified model 较高M Higher M 176 27 6498 331161 S4 中等M Middle M 176 28 5938 352740 S5 较低M Lower M 176 30 4926 402102 S6 *表示模型拟合的计算机处理器为Intel Core i5 2.4 G * indicated the processor of computer for model fit was Intel Core i5 2.4 G

表 3 大眼金枪鱼SS3模型参数个数及拟合时间比较 Table 3 Comparison of numbers of parameters and the fitting time of SS3 model for big-eye tuna

复杂模型拟合估算的参数达234个，简化后参数个数降为176个，总体来看，拟合时间缩短1/2以上(表 3)。同样的模型结构，陡度和自然死亡系数的不同水平对拟合时间影响不大，除了h=0.9时的简化模型(S2)，拟合时间也会受参数初始值的影响。表 3同时给出了资源的2个重要尺度参数(Scaling parameter)：原始补充量和原始亲体量，这2个变量反映了整个资源的最初资源量。相对于复杂模型，在相同的h或M假设下，简化模型对R₀、SSB₀均高估11%-15%左右。

资源评估得到的主要变量时间序列包括资源量、补充量、亲体量、捕捞死亡系数、渔获量等。结果显示，复杂模型和简化模型对这些变量的总体变化趋势的“描述”是一致的，即简化模型能较好地描述大眼金枪鱼资源动态的整体变化趋势，但在一些具体年份的估算值有所不同。限于篇幅，本研究仅给出h=1.0时的补充量、亲体量和捕捞死亡系数(图 2-图 4)。简化模型未能更好地描述早期(1975-1983年第1季度)的补充量变化，但后期估算较好(图 2)。简化模型低估了1991年之前的亲体量，而高估了1991年之后的亲体量，但除了起始年之外，简化模型基本上能较好地描述亲体量的动态变化(图 3)。对捕捞死亡系数的估算则与亲体量呈相反的趋势，简化模型高估了1991年之前的捕捞死亡系数，但低估了1991年之后多数年份的捕捞死亡系数(图 4)，这与亲体量的变化相吻合(图 3)，即高捕捞死亡系数导致了资源量的降低，反之亦然。

图 1(Fig. 1)

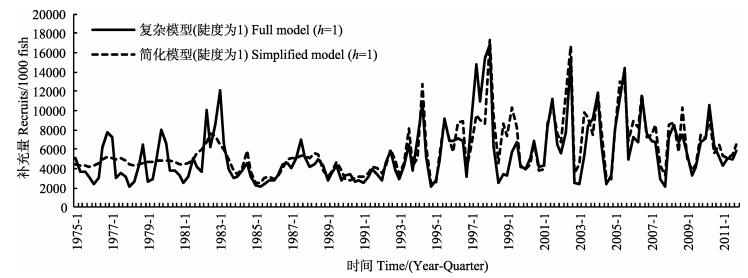
图 2 大眼金枪鱼补充量时间序列 Figure 2 Recruit time series of big-eye tuna

图 1(Fig. 1)

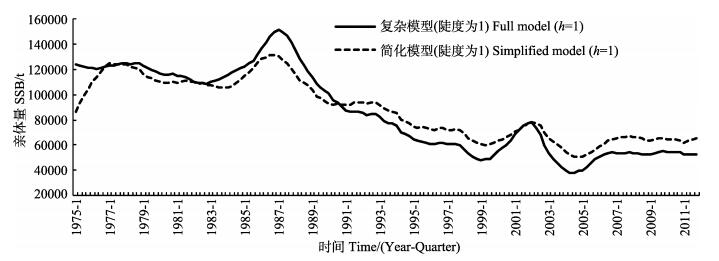
图 3 大眼金枪鱼亲体量时间序列 Figure 3 Spawning stock biomass (SSB) time series of big-eye tuna

图 1(Fig. 1)

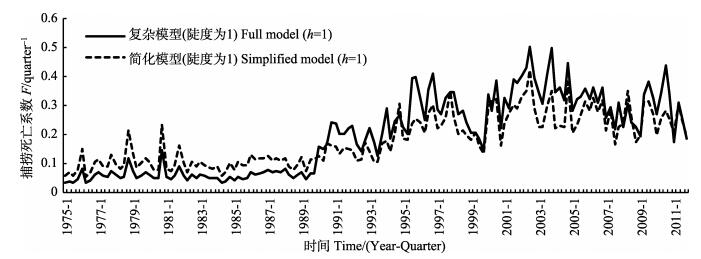
图 4 大眼金枪鱼捕捞死亡系数时间序列 Figure 4 Fishing mortality time series of big-eye tuna

从重要的生物学参考点看(表 4)，简化模型对MSY的低估较大(约30%)，对SSB_MSY/SSB₀的低估量为14%-37%，对F_curr/F_MSY的低估量为10%-21%。对其余4个参考点均予高估，其中，对F_MSY高估1%-20%，F_multiplier高估11%-27%，C_curr/MSY高估41%-53%，SSB_curr/SSB_MSY高估46%-84%。不同的h或M假设水平下，简化模型对这些参考点的估算能力有差异，但未改变“高估”或“低估”的趋势(表 4)。总体而言，无论是复杂模型还是简化模型，参考点估算值受M的影响略小于h，但也会受h和M不同假设水平变化的影响。

表 4(Tab. 4)

表 4 复杂模型和简化模型估计的生物学参考点比较 Table 4 Comparison of biological reference points of the full model and the simplified model 模型Model 假设Assumption MSY (t) FMSY Fmultiplier SSBMSY/SSB0 Ccurr/MSY Fcurr/FMSY SSBcurr/SSBMSY 复杂模型 Full model 陡度h=1.0 95636 0.25 1.69 0.23 0.79 0.59 0.77 陡度h=0.9 95352 0.20 1.39 0.27 0.79 0.72 0.63 陡度h=0.8 96360 0.17 1.18 0.30 0.79 0.85 0.54 简化模型 Simplified model 陡度h=1.0 67724 0.27 2.12 0.14 1.12 0.47 1.38 陡度h=0.9 66204 0.20 1.59 0.21 1.14 0.63 0.94 陡度h=0.8 66320 0.17 1.31 0.26 1.14 0.76 0.79 复杂模型 Full model 较高M Higher M 95636 0.25 1.69 0.23 0.79 0.59 0.77 中等M Middle M 94552 0.23 1.67 0.23 0.80 0.60 0.73 较低M Lower M 93276 0.21 1.60 0.24 0.81 0.63 0.57 简化模 Simplified model 较高M Higher M 67724 0.27 2.12 0.14 1.12 0.47 1.38 中等M Middle M 65484 0.26 2.09 0.15 1.16 0.48 1.27 较低M Lower M 61252 0.26 2.03 0.16 1.24 0.49 1.05

表 4 复杂模型和简化模型估计的生物学参考点比较 Table 4 Comparison of biological reference points of the full model and the simplified model

由于参考点的类型较多，实践中常根据F_curr/F_MSY和SSB_curr/SSB_MSY绘制Kobe图来判断资源开发状态。大眼金枪鱼的Kobe图见图 5。从图 5可以看出，简化模型S1、S4、S5、S6 (表 3)落在右下区，该区内F_curr/F_MSY < 1，而SSB_curr/SSB_MSY > 1，因此，这4个模型认为资源处于“健康”状态；其他8个模型(包括全部复杂模型和2个简化模型)均落在左下区，该区内SSB_curr/SSB_MSY < 1，但F_curr/F_MSY < 1，可以解释为资源刚经历了过度捕捞，有效的管理措施已将F降低(但生物量未来得及恢复)。

图 1(Fig. 1)

图 5 复杂模型和简化模型对大眼金枪鱼资源状态判断的Kobe图 Figure 5 Kobe plot of the evaluation of stock status for big-eye tuna by full models and simplified models

简化模型S2、S3与相应的复杂模型F2、F3对资源判断得出了相同的结论，但S1得出的结论与相应的F1不同(图 5)。这表明简化模型对资源判断的正确性受参数h的影响，在高h值(即补充量受亲体量的制约小)的情况下，简化模型未能准确判断资源状态。这也印证了简化模型S4-S6未能准确判断资源状态，即模型F4-F6和S4-S6均是在h=1.0的假设条件下(S1与S4实际上假设相同)。本研究并非严格意义上的“模拟-验证”试验，故未对h和M的相互影响做交叉试验。

本研究采用的资源评估方法目前称之为“综合分析法”(Integrated analysis)或“综合模型”(Integrated model)。综合分析法可以最大限度地利用源自同一渔业资源的不同类型的数据资料，其本质思想是构建各种不同数据资料的“联合似然”(Joint likelihood) (Maunder et al, 2013)。该数据资料常指年渔获量、渔获年龄组成、渔获长度组成、资源相对丰度指数(可以是商业性渔业或科学调查获得的CPUE等)、标志放流回捕数据等。与实际种群分析等传统方法不同，综合分析法可以允许数据在某些年份缺失。但是，运用该方法不可回避的问题是“划分多少个渔业最合适？”。渔业的划分应满足“相同渔业具有相同的选择性”这一条件。因此，一般趋向于划分较多的渔业，但这需要更多细分的数据支持，模型也就更复杂。即便是像东太平洋大眼金枪鱼这样已经评估几十年的资源，对渔业的划分仍无明确的标准，很多时候是依靠研究者的经验，其评估曾分别采用了13种渔业(Maunder et al, 2003)和23种渔业(Aires-da-Silva et al, 2014) 2种方案。既然捕捞大眼金枪鱼的基本渔具类型是围网(产量极大部分来自人工集鱼作业)和延绳钓(产量大部分来自深水超低温延绳钓)，那么应该可以将渔业类型减少到只有围网和延绳钓2种渔业。

因此，本研究尝试对大眼金枪鱼SS3模型的渔业类型减少到围网和延绳钓2种，从而简化了模型结构。结果显示，简化模型基本能够描述资源的历史变动，但对具体参数值的估计存在误差。SS3模型估算的参数大部分是补充量变化(Deviation)和选择性曲线的参数，除补充量变化外，其他参数在复杂模型和简化模型里已无可比性。简化模型低估了原始补充量和亲体量这2个重要的尺度参数，这可能也导致了其他生物学参考点的估算误差。但简化模型对传统生物学参考点F_MSY的估计较为准确，且受h和M的影响较小(表 4)。参数h对简化模型基于Kobe图判断资源是否过度捕捞的准确性有重要影响。可以确定的是，模型简化的效果评价，与采用的渔业管理生物学参考点和资源状况判断标准的选择有关。

大眼金枪鱼SS3模型简化的主要误差来源有2个，一是简化模型仅采用了复杂模型中源自“渔业2”的围网渔业丰度指数和“渔业16-17”的延绳钓渔业丰度指数，虽然这2个渔业在产量和捕捞区域上具有代表性(即为主要渔场)(Aires-da-Silva et al, 2015)，但这2个指数显然并不能完全“指示”可捕资源量的时间动态；二是根据渔获量对体长组成数据进行加权平均，获得简化模型的体长组成。这样处理导致渔获量高的渔业对体长组成数据的影响越大，但渔获量高的渔业，其体长样本的采样代表性并不一定高。简化模型大大缩短了模型运行时间。在实践中，资源评估需要最大限度的考虑参数和模型结构的不确定性，因此单个模型的运行时间是研究者是必须考虑的问题。例如，近期中西太平洋大眼金枪鱼的资源评估(Harley et al, 2014)，构建了108个模型来比较不确定性因素(如最大体长、自然死亡系数、陡度参数、渔业数据的权重)对评估结果的影响。简化模型结构和提高准确性的权衡(Trade-off)，是今后大眼金枪鱼评估需要研究的问题。

计算机的运用使现代渔业资源评估的方法不断复杂化(Schnute et al, 2007)。在欧洲和北美，在数据资料满足的条件下，综合分析法已成为资源评估的主流方法。综合分析法的优点是在一个模型中可以容纳多种类型的数据，可以确保建模过程中不同假设的一致性(即传递不确定性)，对有关参数和数据权重的影响分析也较为容易(Maunder et al, 2013)；但模型运算时间长、收敛性问题、模型选择、参数的假设和相互影响、结果的解释等问题，也是综合分析法需要优化或解决的问题。况且，当前渔业资源评估建模仍有许多过程问题没有完全解决，即便对于生长与死亡、渔业动态、渔具选择性等最基本问题，仍然需要不断的研究(Maunder et al, 2015)。因此，对综合分析法的简化，将是今后渔业资源评估的重要方向之一。Cotter等(2004)通过对欧洲北海渔业资源的多模型比较评估认为，并非模型越复杂越有利于准确评估，并发现仅利用分年龄组CPUE数据的“年龄组渔获曲线法”(Year-class curve)，其评估的综合表现要优于实际种群分析、状态空间模型等更复杂的模型。Jardim等(2015)甚至提出用简单的线性模型进行多鱼种评估的大胆设想，并已构建了初步的方法框架。