桑沟湾的海带(Saccharina japonica)养殖始于1957年，产量逐年增加，目前己逾10万t (张为先, 1992)。海带养殖产量与海带的长度和重量有关，生长状况较好的海带，长度、宽度和厚度都较大，出成率比较高。近年来，桑沟湾筏式养殖的海带在养殖后期(一般是4月下旬以后)，叶片有明显的枯烂现象，并随时间推移愈加严重，在一定程度上影响了海带养殖产量和效益。Li等(2007)研究表明，海带叶片末梢枯烂的现象从11月放苗开始出现，并持续整个养殖周期。Suzuki等(2008)发现，当温度超过17.5℃，海带叶片末梢的枯烂率就已超过其生长率。同时，温度、光照和营养盐的变化都可能引起海带叶片末梢枯烂。

在过去的几十年里，国内外开发了一些用于模拟海藻生长的模型，一方面用于预测海带和石莼(Ulva rigida)等藻类的生长(Zhang et al, 2016; Solidoro et al, 1997)，另一方面也用于绿藻和蓝藻等灾害藻类暴发的预警(Martins et al, 2002;汪浩等, 2012)。为了更好地模拟环境因素对海带生长的影响，本研究在桑沟湾的3个不同区域设置了采样站位，进行海带采样与环境监测。通过分析海带生长的主要限制因素，将其参数化，以动态能量学(Dynamic Energy Budget, DEB)理论为指导(Marianne et al, 2009)，建立了基于桑沟湾的海带个体生长模型。通过模型运算可以有效预测不同的环境条件下，海带的生长状况和产量变化，为今后海区养殖容量的估算及养殖管理提供理论和技术支持。

1 材料与方法 1.1 研究海域

桑沟湾(37°01'~37°09'N，122°24'~122°35'E)位于山东半岛东部沿海，是我国北方主要的浅海养殖水域之一，为半封闭海湾，呈“C”状。湾口南北宽11.5 km，东西宽7.5 km，海岸线长90 km，面积为144 km²。温度范围2℃~26℃，年平均水温为13℃; 湾内盐度变化不大，平均盐度为31.76;日光照射时数平均为208.4 h，年平均降雨800 mm(国家海洋局一所，1988)。

实验在桑沟湾高区(High Zone，HZ)、中区(Medium Zone，MZ)、低区(Low Zone，LZ)设置了3个采样站，高区：37°8'33.47"N，122°37'59.22"E; 中区：37°8'37.44"N，122°36'30.98"E; 低区：37°09'52.88"N，122°35'10.06"E。其中，高区水深23.4 m，流速较大，为0.3 m/s左右; 中区水深20 m，流速较为适宜，为0.25 m/s左右; 低区水深16.7 m，流速较小，为0.1 m/s左右。所有采样站位均用GPS进行准确定位(图 1)。桑沟湾筏式养殖海带采用间隔平养，养殖期为11月中旬到次年7月中旬。

1.2 桑沟湾海域环境及海带生长参数

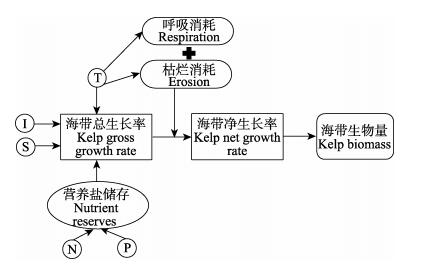
海带个体生长模型的概念流程如图 2所示。实验对桑沟湾海带2016年11月至2017年6月的生长情况和环境条件进行监测。环境监测项目包括水体表面温度T(℃)、水体盐度S、营养盐N和P浓度(μmol/L)、环境光照I (μmol/m²·s)以及颗粒有机物浓度TPM(mg/L)，每30 d左右监测1次。环境参数按照《海洋调查规范》要求采样，海水中营养盐、TPM的分析均按照《海洋监测规范》(GB 17378-2007)进行。海带生长情况监测项目包括干重DW(g)和长度Length(cm)，每30 d左右监测1次，每次测量5个个体。

1.3 模型函数

海带的净生长量(N_growth)由其总生长量(G_growth)与呼吸作用(resp)和海带枯烂(E_kelp)之差决定：

$ N_{\text { growth }}=G_{\text { growth }}-{resp}-E_{\text { kelp }} $

式中，呼吸作用(resp)主要采用Jørgensen等(2008)关于计算呼吸作用的公式：

$ r e s p=R_{\max 20^{\circ} \mathrm{C}} \times \theta^{T-20} $

式中，R_max20℃为20℃最大呼吸速率，θ为经验系数经模型校正取1.02。

G_growth受海带最大生长率(μ_max)、温度(T)的变动、光照的限制(I)、盐度限制(S)及营养物的限制(N、P)共同作用。利用相乘限制方法，即：

$ G_{\text { growth }}=m_{\max } \times f(T) \times f(I) \times f(S) \times f(N P) $

海带的生长遵循在最适温度附近的偏正态分布，所以采用如下温度函数(Radach et al, 1993)：

$ f(T)=exp \left[-2.3 \times\left(\frac{T-T_{\mathrm{opt}}}{T_{\mathrm{x}}-T_{\mathrm{opt}}}\right)^{2}\right] $

式中，T_opt和T_x分别代表海带生长的最适温度和温度生态幅; 当T≤T_opt时，T_x=T_min(温度生态幅下限); 当T＞T_opt时，T_x=T_max(温度生态幅上限)。

海带在高强度的光强下光合作用受到抑制，生长处于抑制状态(张起信, 1994)。因此，光照函数采用Steele公式光抑制模型最优曲线(Steele et al, 1962)：

$ f(I)=\frac{I}{I_{\mathrm{opt}}} \times e^{\left(1-\frac{I}{I_{o p t}}\right)} $

式中，I_opt为光合作用最适光强，I为到达海带表面的光照强度。

潮位的变化会引起光照水深的变化。由于海带为筏式养殖生物，浮筏本身会随着潮水升降，所以潮位的变化并不会引起养殖生物水层的变化，海带基本保持固定的生长水层不变。同时，由于水流的存在，海带基本上是漂浮在水的上层。在深度(Z)光照(I)的变化，用Beer公式(Parsons et al, 1990)表示：

$ I=I_{0} \times exp (-k \times Z) $

式中，I₀为水表面的光强，k为吸光系数，Z为水层深度。

养殖海区水体的初级生产力也取决于水中的吸光系数k。潮位的变化所引起的涨潮、退潮以及风浪流，都能对水体和海床造成扰动。这种变化引起的海底沉积物的再悬浮是引起k变化的主要因素。Suzuki等(2008)在桑沟湾研究得出TPM与k之间的关系，建立经验公式如下：

$ k=0.0484 \times \mathrm{TPM}+0.0243 $

公式描述了k与TPM之间的关系，利用不同时刻的TPM测值输入模型，进一步反映Z深度下的光照变化情况。

光照强制函数的输入，不能以某一天的某一时刻光照作为变量输入，应参考养殖海区的当日平均光照情况，同时需要考虑每月的晴日天、阴雨雪天、当月的日照时长等。根据中国气象局对荣成市2016~2017年的天气预报，计算了每月晴日天及阴雨天数、每月的日照时长; 并且根据实测的桑沟湾海域晴日天及阴雨天光照强度，一天平均海表面光照强度分别为550、385 μmol/m²·s。

平均海表光照强度公式：

$ {I_0}{\rm{ = }}\frac{{日照时长 \times \left({晴日天 \times 550 + 阴雨天 \times 385} \right)}}{{总天数 \times 24}} $

针对桑沟湾盐度变化情况，参照Martins等(2002)浒苔模型中对盐度限制的表达公式：

$ f(S)=1-\left(\frac{S-S_{\mathrm{opt}}}{S_{\mathrm{x}}-S_{\mathrm{opt}}}\right)^{m} $

式中，S_opt为最适生长盐度，当S＜S_opt，S_x=S_min(停止生长的盐度耐受的最小值)，m=2.5;S≥S_opt，S_x=S_max(停止生长的盐度耐受的最大值)，m=2。

海带生长受相对最缺乏的营养盐限制，海带体内氮磷比(N/P)是12~16时，营养盐最易被海带吸收。因此，N/P＜12，f(NP)= f(N); 12≤N/P≤16，f(NP)=1;N/P＞16，f(NP)=f(P)(Martins et al, 2002)。

海带对N营养盐的吸收特征符合饱和吸收动力学。同时，因为藻类的生长取决于细胞内浓度，而不是水体中的浓度，根据Michaelis-Menten(N_int－N_imin)米氏方程计算：

$ f(\mathrm{N})=\frac{N_{\mathrm{int}}-N_{\mathrm{imin}}}{K_{\mathrm{q}}+N_{\mathrm{int}}-N_{\mathrm{imin}}} $

式中，N_int和N_imin分别是海带体内游离N含量、海带体内游离N的最低需求，K_q为N的半饱和同化系数。

海带对PO₄-P的吸收动力学特征不符合米氏方程，藻体的生长随体内P的增加呈线性增加(Jørgensen等，2008)。

如$ P_{\mathrm{int}} <P_{\mathrm{imax}}, f(\mathrm{P})=\frac{P_{\mathrm{int}}}{P_{\mathrm{imax}}}$; 如果P_int≥P_imax，f (P)=1

式中，P_int和P_imax分别是海带体内游离P、维持最大生长率所需的体内游离P含量。

海带体内游离N、P营养盐含量(N_int, P_int)的计算是将吸收的营养盐($ \varphi $)减去同化为组织的营养盐(γ)得到。

$ \begin{array}{c}{\varphi=\frac{X_{\text { imax }}-X_{\text { int }}}{X_{\text { imax }}-X_{\text { int }}} \times \frac{V_{\text { max }} \times X_{\text { ext }}}{K_\text{x}+X_{\text { ext }}}} \\ {\gamma=X_{\text { int }} \times G_{\text { growth }}}\end{array} $

式中，X代表N或P; V_max为N或P营养盐的最大吸收速率; K_x为N或P营养盐吸收的半饱和常数; X_ext为海水中无机N或P营养盐含量。

海带存在由于光照过强引起的白烂病，光照过弱引起的绿烂病等病理性枯烂，这类枯烂可根据光照情况及时调节养殖水层得到改善。除了海带病理性枯烂，海带叶片末梢枯烂也是一种遗传特性，当温度或其他环境条件改变，海带末梢开始枯烂，并通过枯烂组织的营养盐循环，促进海带分生组织的生长，有利于孢子的放散，属于一种生存机制(Li et al, 2007)。在4月以前，海带末梢枯烂并不明显，之后随着海水温度的不断升高，末梢枯烂率大幅度上升，5月枯烂率达到最大，以后保持平稳状态(Li et al, 2007; Mizuta et al, 2003)。综上所述，根据海带的最适温度(T_opt)与海水中的温度(T)之间的差值作为指数，得出海带枯烂的方程：

$ E_{\mathrm{kelp}}=E_{\mathrm{max}} \times P^{\left(T-T_{\mathrm{opt}}\right)} $

式中，T_opt为海带最适生长温度，T为不同时刻的温度测量值，P为经验系数经模型校正，取1.05，E_max为海带最大枯烂率。

吴荣军等(2009)对于海带长度与干重得到的经典公式，可能是存在海带干湿比不同等因素，与作者的海带长度与干重实测值有一定差异。本研究通过Origin 9.0软件对吴荣军海带长度与干重经典公式进行系数校准，得出海带长度与干重经典公式为：

$ L=exp \left[\ln \left(\mathrm{DW} \times 10^{6.28}\right) / 3.35\right] $

式中，L为海带长度，DW为海带干重。

1.4 状态变量及强制函数

模型中的3个状态变量包括海带体内营养盐含量(N_int，P_int，μmol/g)、海带的干重(DW，g)、N_int(t)、P_int(t)、DW(t)：

$ \begin{aligned} N_{\text { int }}(t) &=N_{\text { int }}(t-d t)+\varphi_{\mathrm{N}}-\gamma_{\mathrm{N}} \\ P_{\text { int }}(t) &=P_{\text { int }}(t-d t)+\varphi_{\mathrm{P}}-\gamma_{\mathrm{P}} \\ \mathrm{DW}(t) &=\mathrm{DW}(t-d t)+N_{\text { growth }} \end{aligned} $

模型中状态变量的初始值N_int和P_int的取值，采用海带组织氮TN含量及组织磷TP含量以海带干重的百分比(% DW)表示(王文雷等, 2009)。Zhang等(2016)测定1月海带TN为1.51%，经过单位换算为N_int=1071 μmol/g。刘嘉伟等(2017)测定海带TP为0.218%，经过单位换算为P_int=70.32 μmol/g。

强制函数(Forcing functions)也称为外部变量，它是影响生态系统状态的外部变量或函数。模型可以用来预测强制函数随时间变化时，生态系统的状态将产生何种变化和影响。水温T(℃)、光照I(μmol/m²·s)、水体N含量N_ext(μmol/L)(包括NH₄⁺-N和NO₃^–-N)、水体中的PO₄^3–-P含量P_ext(μmol/L)、水体中颗粒物浓度TPM(mg/L)为模型的强制函数，根据不同时刻的实测值输入。

1.5 模型中的参数

模型总共包含22个常变量(表 1)，与营养盐吸收消耗相关参数为11个，海带生长消耗相关参数3个，海带生长环境相关参数8个。模型中大部分重要参数来自桑沟湾海区实验研究结果及相关文献。

海带孢子体适温范围很广，最适温为5~10℃，结合养殖生产实际，适温范围约在12~13℃左右(张为先等, 1992;曾呈奎等, 1994)，模型选择海带生长最适温度T_opt为12℃，T_min为0.5℃，T_max为20℃。

季仲强(2011)研究不同盐度下海带对N、P营养盐的吸收效率表明，盐度为3时，P的吸收出现了负吸收现象。陈根禄(1958)提出，盐度为29~32最适宜海带生长。因此，设S_min为3，盐度上限S_max为40，最适盐度S_opt设为30。张起信(1995)设定的I_opt范围为252~ 396 μmol/m²·s，Duarte等(2003)对于I_opt的设定值为491.4 μmol/m²·s，模型设定I_opt为350 μmol/m²·s。

根据沈淑芬(2013)对海带N、P营养盐吸收动力学特征的研究，选取V_maxNO3、V_maxNH4、V_maxPO4分别为10.28、52.63、8.58 μmol/g·h，经单位换算分别为246.72、1263.12、205.92 mmol/g·d，对应的K_NO3、K_NH4、K_PO4分别为29.02、169.49、6.01 μmol/L。N含量为干重的2.4%，1.3%分别为N_imax和N_imin，经单位换算及模型率定设为1714 μmolN/gDW和300 μmolN/gDW (Mizuta et al, 1992)。P_imax和P_imin选取171 μmolP/gDW和30 μmolP/gDW (Mizuta et al, 2003)。K_q和R_max20℃参数值取自EPA(1985)并进行模型校正。

海带一般是漂浮在水中，1月开始加入浮球，提升海带的养殖水层，使海带分生组织基本保持在50 cm左右水层，因此，选择Z为0.5 m。

姚海芹(2016)测量海带平均日生长速率范围在(0.15~0.75)/d之间，根据文献及模型调试选取0.6/d为海带的最大生长率。针对海带枯烂率研究表明，海带在整个养殖周期，枯烂的长度约为196 cm，2.0 cm/d为海带最大枯烂率(Mizuta et al, 2003; Li et al, 2007)，枯烂鲜重为(4.0±0.9) gwt/d (Suzuki et al, 2008)，结合此时海带的鲜重，换算成百分比约为0.006/d，假定同一海带各部分的干湿比一致，选择0.006为E_max，海带生长模型中相应参数与取值见表 1。

1.6 模型构建及运行

在海带生长的生理生化过程分析的基础上，利用可视化模型软件Stella Architect 1.4.3构建上述的公式及参数，基于Stella软件构建出海带生长模型流程图(图 3)。其中，模型设置包括时间步长为0.04 d，根据海带养成时间设置模拟时长为220 d。以海带苗的放苗时间为准，低区11月15日，中区11月24日，高区12月7日，高、中、低区分别设定不同的模型运算开始时间。高、中、低区海带干重(DW)的初始值分别为0.5 g、0.45 g、0.25 g。

2 结果与分析 2.1 环境实测值

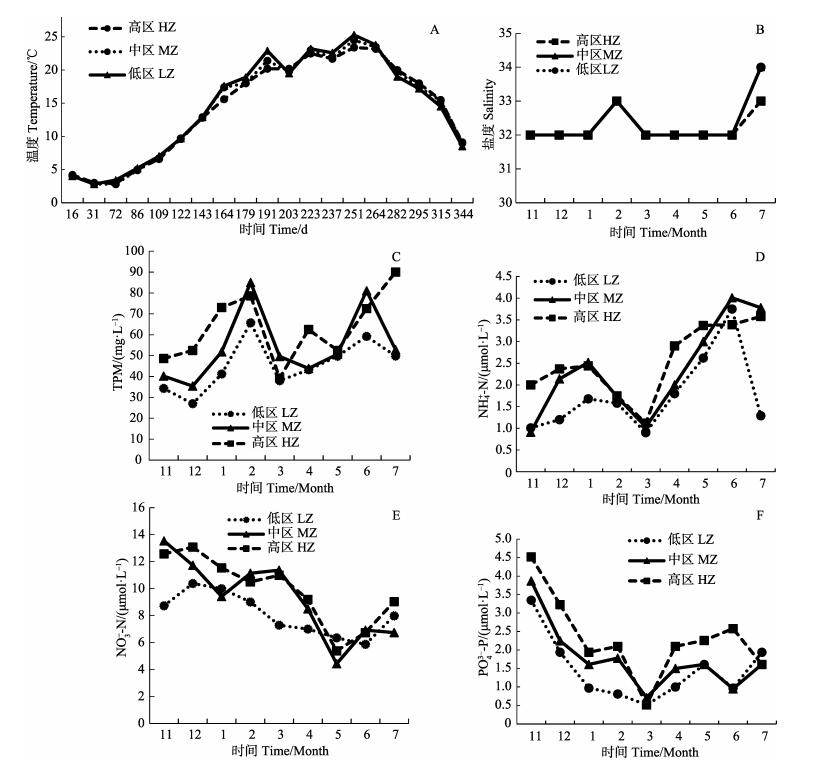
图 4为桑沟湾高、中、低区2016年11月到2017年6月的环境实测值，包括温度、盐度、TPM、营养盐(氨氮NH₄⁺-N、硝酸盐NO₃^–-N、磷酸盐PO₄^3–-P)。在海带养殖期内，低区的温度略高于中、高区。高区的营养盐较中、低区含量丰富，另一方面高区在桑沟湾养殖区外侧，流速较大，水体中颗粒物浓度也较其他区域高。

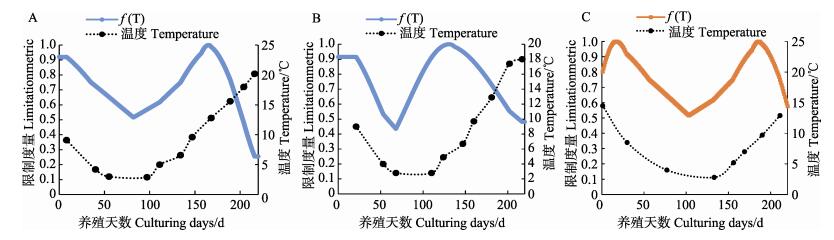
养殖区域温度是养殖生物必须考虑的关键环境因素。不同藻类均有其最适宜生长温度，温度高于或低于养殖生物最适宜生长温度，都有可能造成胁迫，引起细胞膜结构破坏，抑制养殖生物生长，从而造成个体损伤甚至死亡(Sies et al, 1993)。图 5是模型温度强制函数的输出曲线。海带最适生长温度为12℃，海带苗刚下海时海水温度为15℃左右，超过了海带的最适宜生长温度，随着天气逐渐转冷，达到了海带适宜生长温度，3月开始温度逐步升高，5月中旬左右达到12℃，随后温度开始持续攀升，对海带生长的限制作用加强，直到6月中旬左右食品海带收获结束。

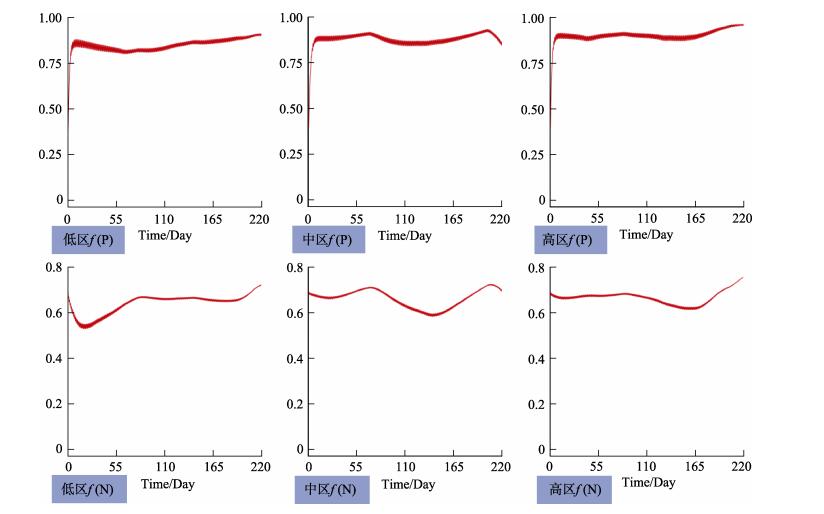
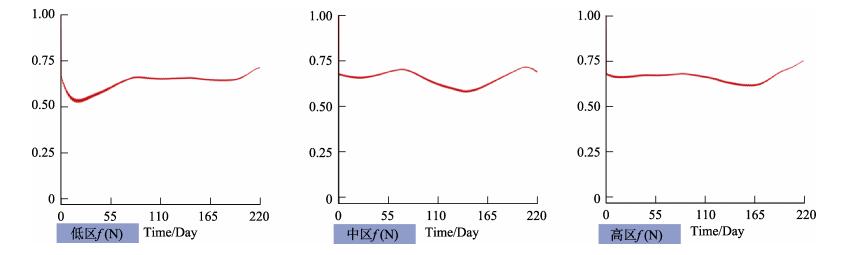
养殖区域的营养盐对于海带的生长起着至关重要的作用，营养盐偏低在一定程度上限制了养殖容量，大面积的养殖生物及养殖筏架影响了养殖区域的水交换，使外部的营养盐难以进入湾内，成为限制水体生产力的关键因素。水体中P含量较少，海带生长内部所需的P也很少，氮磷比符合海带生长的条件，根据图 5所示，f (P)的值稳定在0.8~0.9，f (N)的值稳定在0.54~0.75，图 7所示f (NP)的值稳定在0.54~1。尽管水体中的N、P浓度很低，但是沉积物不断提供的N、P仍然可以满足海带生长的需要，削弱了水体中N、P含量低对海带的限制作用。

桑沟湾太阳辐照冬季辐射最低，春季不断攀升，夏季达到最大值，秋季随之下降。太阳辐射通过养殖水体又经过光的反射、散射损失大部分光能，海带可利用的光能大幅度减少，可见光(400 nm~750 nm)的总能量衰减了58%，只有42%光照总能量可被海带所利用进行光合作用(Ferreira et al, 1989)。适宜的流速也使海带大部分时间均处于漂浮状态，以利于提高海带的受光面积，提高海带的产量。

桑沟湾盐度四季保持在32左右，接近海带生长最适盐度30，对海带生长限制较小，盐度强制函数f (S)保持在0.91~0.96常数。鉴于盐度在桑沟湾海带生长过程中起的限制作用较小，在模型构建上也可忽略盐度这一环境因素对海带生长的影响，而对于一年中盐度变化较大的海域，例如，南方降水量大，盐度变化明显，或是盐度对于养殖生物影响较大的物种进行模型构建时，盐度则是不可或缺的关键环境因素。

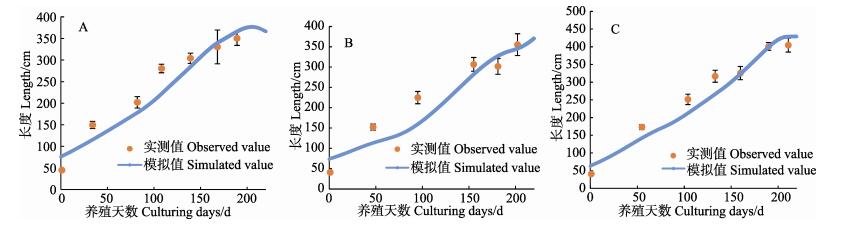
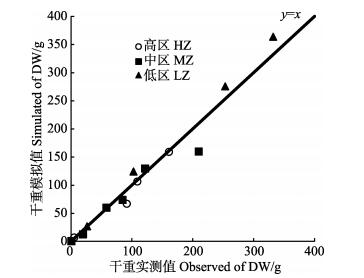
2.2 海带生长模拟值与实测值

高、中、低区海带长度和干重的实测值与模拟值情况如图 8、图 10所示。从模拟生长曲线与海带实测值的比较情况来看，模型可以较好地模拟出海带在不同环境下的长度生长。高、中、低区海带的长度和干重模拟值大部分在实测值的标准误差范围内，能够较好地模拟不同区域海带的一般生长状况。图 9和图 11利用同一时期长度、干重的实测值与模拟值画出散点图，与y=x线性公式拟合，得出R²分别为0.936、0.963。

3 讨论

本研究选取了在水深、温度、光照、流速和营养盐等方面都有较显著差异的高、中、低区3个采样点，作为海带生长模型的预测对象，目的是更加准确地模拟环境因子变化对海带个体生长的影响，进一步验证模型的准确性。以往的藻类生长模型并未考虑同一海域中不同区域的环境差异，因此具有一定的局限性。根据高、中、低区海带生长环境参数以及海带干重、长度的测量结果，我们发现低区比中区的海带生长情况好，高区次之。本研究野外调查发现，高区流速较大，海流的波动对水体和海床扰动使海水浑浊，降低了海带表面的光照强度; 低区风浪较小，水体透明度高，海带受到海水的扰动较少且接收到的光辐照能量较多，有利于干物质的积累。其次，海流较大会使海带边缘较脆嫩的部分发生断折，加速海带叶片的枯烂。此外，不同的养殖区放苗期、收获期不同，高区收获期最晚，此时海水温度较高，可能影响了海带的生长。

海带的叶片枯烂是其特有的重要生理过程，贯穿于整个孢子体生长期，但不同时期的枯烂程度不同(Li et al, 2007)。吴荣军等(2009)的海带生长模型未加入枯烂作用影响，因此，不能很好地反映海带生理过程; Zhang等(2016)对于海带生长模型的研究中虽然考虑了海带枯烂，但只设置了固定的枯烂数值，未考虑环境变化对枯烂的影响，模拟结果不够客观。本研究将海带枯烂作用公式化，建立了海带枯烂与温度的关系，完善了海带枯烂的消耗过程模拟。因此，本研究的模型更加合理。模型在光照强制函数构建过程中，考虑了桑沟湾养殖区全年的晴日天、阴雨天以及日照时长的影响，使光照更为接近桑沟湾的实际情况，这也是其他藻类模型所忽略的一项。

本研究建立的海带个体模型可以较好地模拟海带在不同环境条件下的生长状况。其中部分模拟值在生长后期略低于实测值，推测是海带在生长后期藻体叶片较为宽大，产生光照自遮蔽效应。与此同时，模型中未加入流速对于海带个体生长过程的影响，有可能影响了模型的准确性。张定民等(1986)发现，流速0.01~0.83 m/s为海带生存范围，而实测桑沟湾海区的流速为0.1~0.5 m/s，应不会对本研究中海带个体生存造成影响。但是流速对海带长度、干重等具体生长情况的影响迄今未见报道。为了改进和完善个体生长模型，尚需对流速作用于海带生长过程的机理做进一步研究。

模型中的参数主要根据文献中的数据进行校正，部分文献中参数研究区域不在桑沟湾，由于环境条件存在一定差异，有可能会导致部分模拟值与实测值的偏差。我们认为，模型的建立要综合考虑环境因素并结合模拟物种生物学特征以确定相关参数，从而更好地发挥模型的预测作用。

目前，本研究中建立的海带个体生长模型可作为子模型整合到模拟桑沟湾水产养殖生态系统的综合模型中，为实现基于桑沟湾生态系统的水产养殖空间规划管理提供技术支持。