2. 大连海洋大学 农业农村部北方海水增养殖重点实验室 大连 116023
2. Key Laboratory of Mariculture & Stock Enhancement in North China's Sea, Ministry of Agriculture and Rural Affairs, Dalian Ocean University, Dalian 116023
仿刺参(Apostichopus japonicus)是中国传统的海珍品之一,营养价值高,药用价值广泛(常亚青等, 2004)。海参养殖业在我国经过十几年的迅猛发展,已成为海水养殖的主要产业之一(王秀利等, 2006)。然而,由于刺参养殖的过速发展和不规范运作,基础研究滞后于刺参养殖产业的发展,加之基础设施、养殖工艺和方式的滞后,出现刺参病害频发、种质资源匮乏、成品参品质下降、单位面积产量和产值下降等问题(李成林等, 2010; 张春云等, 2004; 常亚青等, 2006; 赵帅等, 2016);野生资源过度捕捞和养殖刺参长期近亲繁殖、累代养殖,也使刺参品种质量逐步下降(封岩, 2019),刺参的养殖业面临严重威胁。随着人们对仿刺参需求量的增加,迫切需要对其进行遗传改良,选育具有优良性状的新品种。遗传参数的估计是水产动物选择育种的一项基础工作,其中,遗传力是衡量育种进展和育种方法的关键性指标(Falconer et al, 2000)。
遗传力反映亲属间的相似程度和对人工与自然选择的反应速度,往往是育种工作的第一步。传统方法利用亲缘关系较近的个体表型间的相关系数及亲缘系数计算遗传力(Lstibůrek et al, 2018; 文超良等, 2019),在仿刺参遗传力估计中被广泛应用,例如,对仿刺参前期浮游阶段耳状幼体体长(栾生等, 2006)、耳状幼体和稚参体长(李云峰等, 2009)、幼参4个生长性状(孟思远等, 2010)的遗传力估计等。传统方法利用系谱信息构建亲缘相关矩阵(Numerator relation- ship matrix, A阵),并利用线性混合模型估计遗传力,对系谱信息的准确性和完整性要求较高(李晶等, 2020);由于孟德尔抽样误差(Hill, 2014),基于系谱推断的个体间亲缘关系准确性有限,并且存在系谱记录错误、部分群体系谱信息不完整或缺失的情况,使得传统法估计遗传力的准确性存在一定的局限。
随着测序技术的发展,越来越多的学者利用单核苷酸多态性(SNP)分子标记推断个体间的亲缘关系(Thompson, 1975; Lynch, 1988; Queller, 1989),通过构建基因组亲缘关系矩阵(Genomic relationship matrix, GRM)(Li et al, 2014; 文超良等, 2019),进行基于SNP分子标记的遗传力估计(SNP遗传力)(Yang et al, 2017),并在动植物以及人类群体中得到广泛应用(Ritland et al, 1996; Mousseau et al, 1998; Thomas et al, 2002; Visscher et al, 2006)。例如,Yang等(2010)利用REML分析方法估计了SNP数据集解释的人类身高表型的变异程度;Guo等(2018)利用GCTA的REML估计了栉孔扇贝(Chlamys farreri)的生长性状(扇贝长、宽、高和湿重)的SNP遗传力;Fishback等(2002)使用REML方法估计了虹鳟(Oncorhynchus mykiss)总长和重量的遗传力。Benjamin等(2012)将这种基于GRM的REML分析方法称为GREML法。GREML法可以利用SNP数据估计无亲缘关系的个体之间的遗传关系,然后,由全基因组SNP解释的表型变异比例推断遗传力。与传统方法相比,REML分析法适用于非均衡资料的方差组分估计,可大大提高方差组分的估计准确性。本研究利用已完成测序的仿刺参基因组(Li et al, 2018),对不同养殖地理位置仿刺参群体进行全基因组重测序,并针对仿刺参重要经济性状疣足数量,进行全基因组水平的SNP遗传力估计,为丰富仿刺参生长相关的分子育种理论、加快仿刺参优良品种的选育提供一定的理论依据。
1 材料与方法 1.1 仿刺参样本与表型本研究215个仿刺参样本分别来自于8个不同的养殖地理位置:平岛、西小磨、山东栖霞口、蚆蛸岛、中俄杂交仿刺参、旅顺、黄龙尾和俄罗斯海参崴。首先,对所有仿刺参样本的疣足数量进行统计(表 1)。
|
|
表 1 仿刺参样本表型统计 Tab.1 Statistics of papillae number for A. japonicus |
按照动物组织基因组DNA提取试剂盒(天根,北京)说明书提取仿刺参基因组DNA。使用NanoDrop- 2000超微量紫外分光光度计进行定量分析。
检验合格的DNA片段经末端修复、加polyA尾、加测序接头、纯化和PCR扩增完成整个文库制备。库检合格的文库通过Illumina Hiseq Xten的PE150bp模式进行测序,每个样品测序深度为10×。对测序获得的测序数据进行质量过滤,使用Cutadapt软件(Martin, 2011)去除接头序列,使用SolexaQA软件(Cox et al, 2010)去除质量值低于20的碱基,将得到的高质量测序数据利用BWA软件(Li et al, 2009)比对到仿刺参参考基因组。使用Samtools(Li et al, 2009)进行去重复,GATK(Ye et al, 2009)进行局部重比对,碱基质量值校正等处理以及SNP小片段插入缺失(Small INDEL)的检测,按照条件“QD < 2.0||MQ < 40.0||FS > 60.0||MQRankSum < –12.5||ReadPosRankSum < –8.0”对SNP进行过滤,得到最终的SNP位点集。
筛选SNP是为了在重测序获得的高密度SNP中减少或删除处于高度连锁不平衡的SNP,特别是在有限群体中有相当数量的SNP之间存在高度的连锁不平衡关系,会降低对动物个体遗传参数的估计准确度。本研究采用SNP基因频率的平均欧式距离(Average Euclidean distance, AED) (Wu et al, 2016)来筛选SNPs,挑选出次要等位基因频率(Minor allele frequency, MAF)大于0.05和0.1的50K SNP,在筛选出来的50K SNP中随机均匀挑选不同密度的SNP(SNP数量分别为5K、10K、15K、20K、25K、30K、35K、40K、45K和50K)。
1.3 基于SNP的遗传力估计本研究使用GCTA(Yang et al, 2011)(gcta_ 1.93.2beta版本)的GREML(Genomic relatedness matrix restricted maximum likelihood)中的期望最大约束似然法(EM-REML)、平均信息约束似然法(AI-REML)对仿刺参疣足数量的SNP遗传力进行评估。EM算法是由Dempster等(1977)提出的一种迭代算法,可针对有缺失数据的数据资料,获得参数的最大似然估计值。缺失数据在实际的统计分析中非常普遍,EM算法的基本思想是用缺失数据在给定参数的某个估计值的条件下的期望代替缺失数据,从而将不完全数据变成完全数据,使得似然函数的最大化变得相对简单。REML的AI算法(平均信息算法)由Gilmour等(1995)、Johnson等(1995)和Jensen等(1997)提出,它是将求似然函数最大值的2种常见的Newton-Raphson算法和Fisherxs scoring方法结合起来的一种算法(张勤, 2007)。
GCTA软件的核心即如下所示线性混合模型(Yang et al, 2011):
| $ y = Xb + Wu + e $ |
式中,y表示表型,b表示固定效应协变量的系数,u表示随机效应自变量的系数,这里的随机效应指的是所有SNP位点对表型的效应,e表示随机误差。
其中,u和e服从如下正态分布:
| $ u \sim N\left({0, I\sigma _{\rm{u}}^2} \right) $ |
| $ e \sim N\left({0, I\sigma _{{e}}^2} \right) $ |
I为一个n × n的单位矩阵,n表示样本量。
表型方差用如下公式表示:
| $ {\rm{var}}\left(y \right){\rm{ }} = V = WW\prime \sigma _u^2 + I\sigma _e^2 $ |
| $ {w_{ij}} = {\rm{ }}\left({{x_{ij}}--{\rm{ }}2{p_i}} \right)/\sqrt {2{p_i}(1 - {p_i})} $ |
W为第ij元素的标准化基因型矩阵,xij为第j个个体的第i个SNP的参考等位基因的拷贝数,pi为参考等位基因频率。
GCTA对于样本遗传相似度的定义公式:
| $ {{G_{jk}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \frac{{({x_{ij}} - 2{p_i})\left({{x_{ik}} - 2{p_i}} \right)}}{{2{p_i}\left({1 - {p_i}} \right)}}} $ |
定义所有SNP位点的方差:
| $ \begin{array}{*{20}{c}} {\sigma _G^2 = N\sigma _u^2}\\ {则:\;V = G\sigma _G^2 + I\sigma _e^2} \end{array} $ |
式中,N为SNP位点数,G为个体间的亲缘关系矩阵(GRM)。
定义SNP遗传力的计算公式:
| $ h_{SNP}^2 = \sigma _G^2\left({\sigma _G^2 + \sigma _e^2} \right) $ |
对来自不同养殖地理位置的215个仿刺参样本进行高通量重测序,获得一组高质量SNP。构建GRM矩阵后,使用GCTA的2种遗传参数估计方法(AI-REML和EM-REML),添加协变量的校正,针对仿刺参疣足数量,分别计算不同密度SNP下的SNP遗传力估计值及染色体水平的SNP遗传力估计值。
2 结果与分析 2.1 仿刺参疣足数量的表型数据分布从215个仿刺参样本疣足数量的频率直方图和概率密度曲线(图 1a)可以看出,本研究不同地域的仿刺参疣足数量大致符合正态分布,表明仿刺参疣足数量性状不受地域环境的影响。考虑到图 1a中出现大量疣足数量大于60的个体,且主要集中在中俄杂交仿刺参和俄罗斯海参崴群体中,因此,利用R MASS包中nlminb函数,对215个样本数据进行混合正态分布参数的最大似然估计(图 1b),结果显示,样本疣足数量符合2个正态分布(均值39.8、方差6.79和均值54.35、方差10.9)的最优拟合,说明样本中存在多疣足仿刺参群体情况。进一步把8个不同地域的仿刺参群体分为正常群体(平岛、西小磨、山东栖霞口、蚆蛸岛、旅顺和黄龙尾)与多疣足群体(中俄杂交仿刺参和俄罗斯海参崴),并利用R t.test函数对上述2个群体疣足数量进行t检验,结果差异显著(P < 0.01)。根据上述表型数据分布结果,本研究将不同地域的仿刺参群体分为正常群体与多疣足群体,并在SNP遗传力估计模型设计群体固定效应,以校群体分层对SNP遗传力估计的影响。
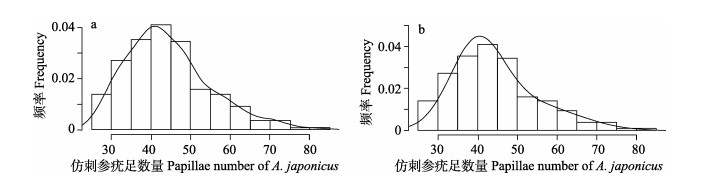
|
图 1 215份仿刺参样本疣足数量的频率直方图和概率密度曲线(a)和双重高斯分布最优拟合(b) Fig.1 True frequency histogram and probability density curve (a) and optimal fitting of a double Gaussian distribution (b) of papillae number for the 215 A. japonicus samples |
本研究全基因组重测序质量较高,GC分布正常,对基因组的覆盖度均超过90%,高质量SNPs数量约为500万个。使用GCTA的2种REML分析方法(EM-REML和AI-REML)对仿刺参疣足数量的遗传力进行评估,比较相同密度、相同次要等位基因频率筛选条件下,不同分析方法得到的仿刺参疣足数量SNP遗传力估计值。发现通过2种方法得到的遗传力估计值差异极小(表 2,表 3),证明本研究采用的分析方法有较好稳定性、可靠性。
|
|
表 2 仿刺参疣足数量SNP遗传力(MAF > 0.05) Tab.2 SNP heritability estimates for papillae number in A. japonicus (MAF > 0.05) |
|
|
表 3 仿刺参疣足数量SNP遗传力(MAF > 0.1) Tab.3 SNP heritability estimates for papillae number in A. japonicus (MAF > 0.1) |
除此之外,本研究对不同密度SNP条件下的仿刺参疣足数量SNP遗传力估计值进行比较,结果显示,当MAF > 0.05时(表 2),不同密度SNP条件下得到的仿刺参疣足数量SNP遗传力估计均值为(0.566± 0.022)~(0.612±0.003),SNP数量在5K、10K时,得到的SNP遗传力估计均值分别为0.567±0.022、0.588± 0.011(AI-REML)和0.566±0.022、0.587±0.011(EM- REML);SNP数量在15K~50K时,得到的遗传力估计均值相较于低密度SNP遗传力估计均值更大,且趋于稳定;SNP数量为50K时,得到的SNP遗传力估计均值最高,分别为0.612±0.003(AI-REML)和0.611±0.003(EM-REML)。当MAF > 0.1时(表 3),不同密度SNP条件下得到的仿刺参疣足数量SNP遗传力估计均值为(0.586±0.015)~(0.615±0.016),SNP数量在5K、10K、15K时,得到的遗传力估计均值分别为0.593±0.026、0.596±0.017、0.587±0.014(AI-REML)和0.592±0.026、0.595±0.017、0.586±0.015(EM- REML);SNP数量在20K~50K时,得到的遗传力估计均值相较于低密度SNP遗传力估计均值更大,且趋于稳定;SNP数量为30K时,得到的SNP遗传力估计均值最高,分别为0.615±0.016(AI-REML)和0.614±0.016 (EM-REML),并且当SNP数量在35K、40K、50K时得到的遗传力估计均值均达到0.614。
2.3 仿刺参疣足数量染色体水平SNP遗传力估计根据已发表的仿刺参基因组和遗传连锁图谱,共发现22个连锁群(Tian et al, 2015; Li et al, 2018),本研究将Scaffold拼接到染色体水平,并对仿刺参疣足数量进行染色体水平的SNP遗传力估计,对染色体SNP遗传力估计值和染色体长度进行回归分析(图 2),结果显示,7号染色体的SNP遗传力估计值最小,为0.085(MAF > 0.05)、0.094(MAF > 0.1);2号染色体的SNP遗传力估计值最大,为0.598(MAF > 0.05)、0.599(MAF > 0.1);14号染色体长度最小,SNP遗传力估计值为0.269(MAF > 0.05)、0.282(MAF > 0.1);1号染色体长度最大,SNP遗传力估计值为0.522(MAF > 0.05)、0.526(MAF > 0.1)。在MAF > 0.05和MAF > 0.1条件下,单个染色体的贡献和其长度显著相关,较长的染色体具有明显的线性趋势(P < 0.05),且遗传力估计值最小的7号染色体和长度最小的14号染色体均偏离线性回归较远。
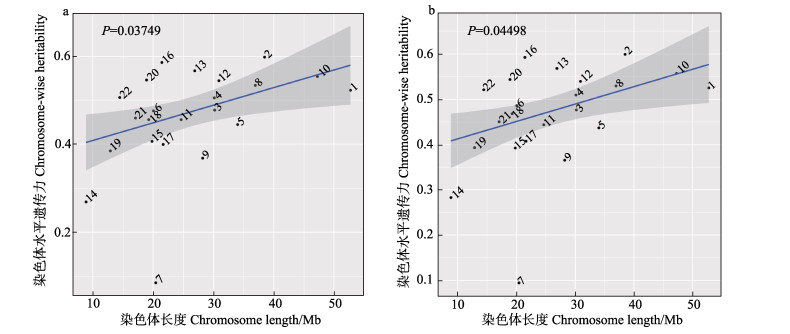
|
图 2 仿刺参疣足数量染色体水平SNP遗传力估计 Fig.2 Chromosome-wise heritability estimates for papillae number in A. japonicus a:MAF > 0.05;b:MAF > 0.1。数字表示每个染色体的遗传力点估计值;实线表示染色体遗传力对染色体长度的线性回归 The numbers show the heritability point estimates of each chromosome. The solid lines plot the linear regression of chromosome-wise heritability against chromosome length |
遗传力是反映性状遗传能力大小的重要遗传参数,准确合理的遗传参数估计有助于更好地理解遗传因素对特定群体某一性状的表型影响程度。估计动物个体的SNP遗传力,首先需要筛选出一组适用的SNP。筛选这些SNP,一般需要满足两个条件:第一,筛选的SNP是该物种基因芯片中共同的SNP,这样可以很方便地将这些基因SNP芯片用于分子育种,而不需要重新设计新的芯片或增加芯片中的SNP位点;第二,选出的SNP有较高的信息含量,其统计准确度要高。Hulsegge等(2013)采用LD的r2 > 0.30作为删除SNP的尺度,结果表明,在保持相同准确性的前提下,使用这个尺度来筛选SNP,可以明显降低所需SNP标记的数量。同时,需要筛选信息量高的SNP,筛选高信息量的SNP可以依据不同的统计指标。例如,Hulsegge等(2013)分别使用Delta(群体间等位基因频率的绝对差异)、Wright(1978)的FST以及Weir等(1984)的FST衡量标记信息量的效果。信息熵(Entropy)(Mitt et al, 2017)也是衡量SNP信息量的指标。本研究采用SNP基因频率的平均欧式距离(Average Euclidean distance, AED) (Wu et al, 2016)来筛选SNPs。后续工作将根据上述指标,挑选信息含量高并可进行准确的遗传参数估计的低密度SNP标记。
群体的分层效应会对遗传力估计值的准确性产生影响。本研究根据215个仿刺参样本疣足数量的频率直方图和概率密度曲线(图 1)初步将研究样本分为两大类,一类为来自中国的品种(正常群体),另一类为俄罗斯以及中国与俄罗斯杂交的品种(多疣足群体)。计算时使用群体分层这一因素作为协变量进行校正,并得到了稳定结果,证明本研究使用的分组依据可靠。本研究使用了基于GCTA的期望最大约束似然法(EM-REML)和平均信息约束似然法(AI-REML)对仿刺参疣足数量的SNP遗传力进行估计,由估计值结果(表 2、表 3)可知,此方法得到的SNP遗传力估计值均具有较高的稳定性和可信度。此前,孟思远等(2010)通过建立家系,使用传统方法估算仿刺参幼参阶段肉刺数目的遗传力,得到仿刺参肉刺(疣足)数量遗传力为0.191~0.404。本研究使用GCTA的REML分析法得到了与传统方法相比更高、更稳定的遗传力估计值,说明疣足数量主要受加性效应的控制,对仿刺参的选择育种具有较大潜力。通过比较不同SNP密度下仿刺参疣足数量SNP遗传力估计值,发现当SNP数量在50K时,得到的遗传力估计值均已达到稳定,说明50K SNP的密度足够捕获数量性状基因座(QTL)大效应和小效应,证实了低密度SNP用于准确估计遗传参数的可行性。同时,在全基因组选择方面,Wu等(2016)通过设计牛的低密度SNP芯片,对育种值估计的准确性进行评估,获得了较准确的结果,也证实了低密度SNP芯片应用于分子育种的可靠性。由于全基因组分析对样本量要求较高,通常在500以上(Yang et al, 2010),本研究的样本量为215,统计量较少,容易导致统计结果出现一定程度的偏差,但所得结果与已报道数据(孟思远等, 2010; 和飞等, 2017)一致。后续工作将扩大样本统计量进行仿刺参数量性状的遗传力评估。
本研究在染色体水平对仿刺参疣足数量SNP遗传力进行估计(图 2),提供性状遗传结构的信息。结果显示,仿刺参疣足数量是一个复杂的数量性状,不同染色体上的变异导致了仿刺参疣足数量的变异,与该性状相关的效应位点散布在各染色体上,说明了通过重测序的技术手段,在全基因组上寻找SNP的重要性。单个染色体的贡献和其长度显著相关,表示在每条染色体上可能有多个小到中等效应的变异,而不是少数具有主要效应的变异。Goddard等(2009)关于家畜复杂性状的分子标记辅助选择结果也支持这一假设,该报道称,性状变异有很大的遗传因素,但由于统计力量不足,大多数具有小到中度影响的变异尚未在遗传关联分析中被确认。而GCTA可以克服分子标记辅助选择的缺陷,通过全基因组标记面板,所有QTL都能和至少1个marker处于连锁不平衡状态。分析发现,7号染色体虽不是最小染色体,但其遗传力估计值最低,与此相反,2号染色体虽不是最大染色体,却具有最大遗传力估计值,说明较大的基因效应位点可能不在7号染色体上,而位于2号染色体,意味着QTL出现在2号染色体的概率较大,出现在7号染色体上的概率较小。此结果的发现为将来开展仿刺参疣足数量的全基因组关联分析(GWAS)提供了支持。
4 总结本研究对不同养殖地理位置仿刺参群体进行全基因组重测序,并针对仿刺参重要经济性状疣足数目,使用GCTA软件的GREML进行全基因组水平的SNP遗传力估计,染色体水平SNP遗传力估计,同时比较不同密度SNP标记条件下的仿刺参疣足数量SNP遗传力估计值;结果表明,仿刺参疣足数量SNP遗传力为中等遗传力(MAF > 0.05时,0.566~0.612;MAF > 0.1时,0.586~0.615),当SNP数量在50K时,得到的遗传力估计值均已达到稳定,且染色体SNP遗传力与其长度显著相关;说明仿刺参疣足数量是复杂数量性状,由全基因组水平多基因共同作用,且50K SNP密度足够捕获QTL大效应和小效应。本研究通过分子学研究方法得到可靠的遗传力估计值,有效解决了传统方法系谱记录繁琐,遗传力估计准确性差等问题,为分子育种技术提供了一定理论依据;同时,证明低密度SNP标记用于仿刺参分子育种的可能性,可为低密度SNP芯片的设计开发提供支持。
Benjamin DJ, Cesarini D, van der Loos MJ, et al. The genetic architecture of economic and political preferences. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(21): 8026-8031 DOI:10.1073/pnas.1120666109 |
Chang YQ, Ding J, Song J, et al. Biological research and culture of sea cucumber and sea urchin. Beijing: Ocean Press, 2004 [常亚青, 丁君, 宋坚, 等. 海参、海胆生物学研究与养殖. 北京: 海洋出版社, 2004]
|
Chang YQ, Sui XL, Li J. The current situation, problem and prospect on the Apostichopus japonicus aquaculture. Fisheries Science, 2006, 25(4): 198-201 [常亚青, 隋锡林, 李俊. 刺参增养殖业现状、存在问题与展望. 水产科学, 2006, 25(4): 198-201 DOI:10.3969/j.issn.1003-1111.2006.04.010] |
Cox MP, Peterson DA, Biggs PJ. SolexaQA: At-a-glance quality assessment of Illumina second-generation sequencing data. BMC Bioinformatics, 2010, 11: 485 DOI:10.1186/1471-2105-11-485 |
Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 1977, 39(1): 1-38 DOI:10.1111/j.2517-6161.1977.tb01600.x |
Falconer DS, Mackay TFC. Introduction to quantitative genetics. Beijing: China Agricultural Science and Technology Press, 2000 [Falconer DS, Mackay TFC. 数量遗传学导论. 4版. 北京: 中国农业科技出版社, 2000]
|
Feng Y. Family construction, expression of growth-related genes and transcriptome analysis of body wall tissue in Apostichopus japonicus. Masterxs Thesis of Dalian Ocean University, 2019 [封岩. 刺参(Apostichopus japonicus)家系构建、生长相关基因的表达及体壁组织的转录组分析. 大连海洋大学硕士研究生学位论文, 2019]
|
Fishback AG, Danzmann RG, Ferguson MM, et al. Estimates of genetic parameters and genotype by environment interactions for growth traits of rainbow trout (Oncorhynchus mykiss) as inferred using molecular pedigrees. Aquaculture, 2002, 206(3): 137-150 |
Gilmour AR, Thompson R, Cullis B. Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics, 1995, 51(4): 1440-1450 DOI:10.2307/2533274 |
Goddard ME, Hayes BJ. Mapping genes for complex traits in domestic animals and their use in breeding programmes. Nature Reviews Genetics, 2009, 10: 381-391 DOI:10.1038/nrg2575 |
Guo HB, Zeng QF, Li YP, et al. Estimating realized heritability for growth in Zhikong scallop (Chlamys farreri) using genome-wide complex trait analysis. Aquaculture, 2018, 497: 103-108 DOI:10.1016/j.aquaculture.2018.07.046 |
He F, Wang YG, Liao MJ, et al. Estimation of the heritability of three economic traits in 9-month-old sea cucumber Apostichopus japonicus. Progress in Fishery Sciences, 2017, 38(5): 114-121 [和飞, 王印庚, 廖梅杰, 等. 刺参(Apostichopus japonicus) 9月龄主要经济性状遗传力的估计. 渔业科学进展, 2017, 38(5): 114-121] |
Hill WG. Applications of population genetics to animal breeding, from Wright, Fisher and Lush to genomic prediction. Genetics, 2014, 196(1): 1-16 DOI:10.1534/genetics.112.147850 |
Hulsegge B, Calus MP, Windig JJ, et al. Selection of SNP from 50K and 777K arrays to predict breed of origin in cattle. Journal of Animal Science, 2013, 91(11): 5128-5134 DOI:10.2527/jas.2013-6678 |
Jensen J, Mantysaari EA, Madsen P, et al. Residual maximum likelihood estimation of (Co)variance components in multivariate mixed linear models using average information. Journal of the Indian Society of Agricultural Statistics, 1997, 49: 215-236 |
Johnson DL, Thompson R. Restricted maximum likelihood estimation of variance components for univariate animal models using sparse matrix techniques and average information. Journal of Dairy Science, 1995, 78(2): 449-456 DOI:10.3168/jds.S0022-0302(95)76654-1 |
Li CL, Song AH, Hu W, et al. Status analysis and sustainable development strategy of sea cucumber Apostichopus japonicus Selenka aquaculture industry in Shandong Province. Progress in Fishery Sciences, 2010, 31(4): 126-133 [李成林, 宋爱环, 胡炜, 等. 山东省刺参养殖产业现状分析与可持续发展对策. 渔业科学进展, 2010, 31(4): 126-133 DOI:10.3969/j.issn.1000-7075.2010.04.018] |
Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics, 2009, 25(14): 1754-1760 DOI:10.1093/bioinformatics/btp324 |
Li H, Glusman G, Hu H, et al. Relationship estimation from whole-genome sequence data. PLoS Genetics, 2014, 10(1): e1004144 DOI:10.1371/journal.pgen.1004144 |
Li H, Handsaker B, Wysoker A, et al. The sequence alignment/ map format and SAMtools. Bioinformatics, 2009, 25(16): 2078-2079 DOI:10.1093/bioinformatics/btp352 |
Li J, Wang J, Kang HM, et al. The difference of genetic parameters for carcass and meat quality traits by BLUP and GBLUP methods in Beijing You Chicken. Acta Veterinaria et Zootechnica Sinica, 2020, 51(1): 35-42 [李晶, 王杰, 康慧敏, 等. 基于BLUP和GBLUP方法估计北京油鸡胴体和肉质性状遗传参数的差异. 畜牧兽医学报, 2020, 51(1): 35-42] |
Li YF, Chang YQ, Tian Y, et al. Heritability of early growth traits in larval and juvenile sea cucumber Apostichopus japonicus. Journal of Dalian Ocean University, 2009, 24(1): 30-33 [李云峰, 常亚青, 田燚, 等. 仿刺参耳状幼体和稚参阶段的体长遗传力估计. 大连水产学院学报, 2009, 24(1): 30-33 DOI:10.3969/j.issn.1000-9957.2009.01.006] |
Li YL, Wang RJ, Xun XG, et al. Sea cucumber genome provides insights into saponin biosynthesis and aestivation regulation. Cell Discovery, 2018, 4(Pt B): 956-960 |
Lstibůrek M, Bittner V, Hodge GR, et al. Estimating realized heritability in panmictic populations. Genetics, 2018, 208(1): 89-95 DOI:10.1534/genetics.117.300508 |
Luan S, Sun HL, Kong J. Heritability of auricularia larval body length for sea cucumber Apostichopus japonicus Selenka. Journal of Fishery Sciences of China, 2006, 13(3): 378-383 [栾生, 孙慧玲, 孔杰. 刺参耳状幼体体长遗传力的估计. 中国水产科学, 2006, 13(3): 378-383 DOI:10.3321/j.issn:1005-8737.2006.03.007] |
Lynch M. Estimation of relatedness by DNA fingerprinting. Molecular Biology and Evolution, 1988, 5(5): 584-99 |
Martin M. Cutadapt removes adapter sequences from high- throughput sequencing reads. EMBnet. Journal, 2011, 17(1): 10-12 DOI:10.14806/ej.17.1.200 |
Meng SY, Chang YQ, Li WD, et al. Heritability of four growth traits in juvenile sea cucumber Apostichopus japonicus. Journal of Dalian Ocean University, 2010, 25(6): 475-479 [孟思远, 常亚青, 李文东, 等. 仿刺参幼参阶段4个生长性状遗传力的估计. 大连海洋大学学报, 2010, 25(6): 475-479 DOI:10.3969/j.issn.1000-9957.2010.06.001] |
Mitt M, Kals M, Pärn K, et al. Improved imputation accuracy of rare and low-frequency variants using population-specific high-coverage WGS-based imputation reference panel. European Journal of Human Genetics, 2017, 25(7): 869-876 DOI:10.1038/ejhg.2017.51 |
Mousseau TA, Ritland K, Heath DD. A novel method for estimating heritability using molecular markers. Heredity, 1998, 80(2): 218-224 DOI:10.1046/j.1365-2540.1998.00269.x |
Queller DC, Goodnight KF. Estimating relatedness using genetic markers. Evolution, 1989, 43(2): 258-275 DOI:10.1111/j.1558-5646.1989.tb04226.x |
Ritland K, Ritland C. Inferences about quantitative inheritance based on natural population structure in the yellow monkeyflower, Mimulus guttatus. Evolution, 1996, 50(3): 1074-1082 DOI:10.1111/j.1558-5646.1996.tb02348.x |
Thomas SC, Coltman DW, Pemberton JM. The use of marker- based relationship information to estimate the heritability of body weight in a natural population: A cautionary tale. Journal of Evolutionary Biology, 2002, 15(1): 92-99 DOI:10.1046/j.1420-9101.2002.00372.x |
Thompson EA. The estimation of pairwise relationships. Annals of Human Genetics, 1975, 39(2): 173-188 DOI:10.1111/j.1469-1809.1975.tb00120.x |
Tian ML, Li YP, Jing J, et al. Construction of a high-density genetic map and quantitative trait locus mapping in the sea cucumber Apostichopus japonicus. Scientific Reports, 2015, 5: 14852 DOI:10.1038/srep14852 |
Ventura RV, Miller SP, Dodds KG, et al. Assessing accuracy of imputation using different SNP panel densities in a multi-breed sheep population. Genetics Selection Evolution, 2016, 48(1): 71 DOI:10.1186/s12711-016-0244-7 |
Visscher PM, Medland SE, Ferreira MAR, et al. Assumption-free estimation of heritability from genome-wide identity-by- descent sharing between full siblings. PLoS Genetics, 2006, 2(3): e41 DOI:10.1371/journal.pgen.0020041 |
Wang XL, Shan X, Qiu XM, et al. The polymorphisms of microsatellite DNA from sea cucumber (Stichopus japonicus). Biotechnology Bulletin, 2006(6): 118-121 [王秀利, 单雪, 仇雪梅, 等. 海参微卫星DNA的多态性. 生物技术通报, 2006(6): 118-121 DOI:10.3969/j.issn.1002-5464.2006.06.027] |
Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population structure. Evolution, 1984, 38(6): 1358-1370 |
Wen CL, Sun CJ, Yang N. The concepts and research progress: From heritability to microbiability. Hereditas (Beijing), 2019, 41(11): 1023-1040 [文超良, 孙从佼, 杨宁. 从遗传力到肠菌力: 概念及研究进展. 遗传, 2019, 41(11): 1023-1040] |
Wright S. Evolution and the genetics of populations, Volume 4: Variability within and among Natural Population. Chicago: University of Chicago Press, 1978
|
Wu XL, Xu JQ, Feng GF, et al. Optimal design of low-density SNP arrays for genomic prediction: Algorithm and applications. PLoS One, 2016, 11(9): e0161719 DOI:10.1371/journal.pone.0161719 |
Yang J, Benyamin B, McEvoy BP, et al. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics, 2010, 42(7): 565-569 DOI:10.1038/ng.608 |
Yang J, Lee SH, Goddard ME, et al. GCTA: A tool for genome-wide complex trait analysis. American Journal of Human Genetics, 2011, 88(1): 76-82 DOI:10.1016/j.ajhg.2010.11.011 |
Yang J, Zeng J, Goddard ME, et al. Concepts, estimation and interpretation of SNP-based heritability. Nature Genetics, 2017, 49(9): 1304-1310 DOI:10.1038/ng.3941 |
Ye K, Schulz MH, Long Q, et al. Pindel: A pattern growth approach to detect break points of large deletions and medium sized insertions from paired-end short reads. Bioinformatics, 2009, 25(21): 2865-71 DOI:10.1093/bioinformatics/btp394 |
Zhang CY, Wang YG, Rong HL, et al. Natural resources, culture and problems of sea cucumber worldwide. Marine Fisheries Research, 2004, 25(3): 89-97 [张春云, 王印庚, 荣小军, 等. 国内外海参自然资源、养殖状况及存在问题. 海洋水产研究, 2004, 25(3): 89-97] |
Zhang Q. Calculation methods in animal genetics and breeding. Beijing: Science Press, 2007 [张勤. 动物遗传育种中的计算方法. 北京: 科学出版社, 2007]
|
Zhao S, Huang X, Wang HF, et al. Estimates of repeatability coefficients for papillae number in four populations of sea cucumber (Apostichopus japonicus). Progress in Fishery Sciences, 2016, 37(5): 115-121 [赵帅, 黄旭, 王海峰, 等. 刺参(Apostichopus japonicus) 4个群体棘数的重复力估计. 渔业科学进展, 2016, 37(5): 115-121] |



