渔网是渔业养殖设施的重要组成部分，作为一种复杂的柔性结构，在恶劣的深海环境中极易发生破坏，会对水产养殖业造成经济损失，因此，网衣破损检测是发展深远海渔业养殖的重要关键技术之一。

对水下网衣的破损检测，目前主要有3种方法：一是采用埋线探测法(Wang et al, 2012; Peng et al, 2016)，该方法通过金属导线的通断检测网衣的破损，当网衣破损时，金属线会与海水形成闭合回路，触动警报装置，并报告网箱编号及网衣编号，但这种方法需要在网衣周围安装金属线，这会增加网衣的负荷，容易造成疲劳损伤，从而缩短网衣使用寿命；二是采用声呐检测法(Knudsen et al, 2004)，该方法的工作原理是当网衣系统发生破损有鱼群逃逸时，网箱内外的声波图像会有明显差异，但这种方式无法确定破损位置及破损程度，同时，如果有鱼群围绕网箱周围游动，声呐也会误检为破损，导致检测结果不准确；三是采用图像分析法(Lee et al, 2007; Zhang et al, 2016; Zhao et al, 2020)，该方法是将水下摄像机安装在AUV/ ROV上进行图像采集，检测网衣是否发生破损，该方法对摄像头的像素质量以及水体浑浊程度有极高的要求，不易判断处在浑浊水质中的网衣是否破损。

随着传感器和计算机的快速发展，研究者开始利用数字孪生技术对结构物进行破损检测。数字孪生是物理实体在数字世界的虚拟实体，能根据传感数据对结构物实现状态监测。Kim等(2020)开发了底刺网的数字孪生模型，可通过识别网组件上加速度计的信号变化来检测网衣缆绳的破损以及识别损坏缆绳的位置。Chung等(2020)开发的数字孪生体只需要根据张力腿平台的位移传感器数据就可以进行系泊缆绳的损伤检测。Ritto等(2021)开发了悬臂梁的数字孪生体，可以根据杆件的振动变化来识别杆件的破损位置及破损程度。本研究应用数字孪生方法，结合数值模拟以及人工神经网络技术来开发渔网的数字孪生体，根据网衣的拉力传感数据进行平面渔网的破损检测。

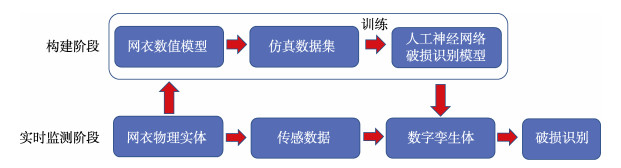
1 材料与方法 1.1 网衣破损检测基本框架

基于数字孪生技术的网衣破损检测的整体框架如图 1所示。首先建立网衣数值模型，考虑各种波浪条件以及网衣的破损情况获得力学仿真数据集；然后建立人工神经网络算法进行网衣破损识别训练，从而构建网衣的数字孪生体。在实时监测阶段，根据网衣物理实体的实时传感数据，数字孪生体可以快速识别网衣是否发生破损。

1.2 网衣物理模型设置

本研究首先进行物理模型实验，采集完整渔网和破损渔网的物理模型数据，用于验证数值模型的正确性及测试数字孪生体检测网衣破损的准确性。所有实验在大连理工大学海岸和近海工程国家重点实验室波浪流水槽内进行。波浪槽长为50.0 m，宽为3.0 m，深为1.0 m。水槽一侧装有多向造波系统、数据采集系统和多台计算机。

图 2为网衣物理模型的实验布置。平面渔网由网衣和4条纲绳组成。网衣宽为0.76 m，高为0.76 m，网线直径为3 mm，网孔大小为20 mm×20 mm。纲绳分为横向纲绳和竖向纲绳。网衣的破损形式如图 3所示。实验在横纲、竖纲上分别安装一个拉力传感器。实验中水深为0.7 m，制造固定水流，测得流速为0.12 m/s。实验采集渔网在不同波浪条件下的拉力传感器数据。

1.3 网衣数值模拟

网衣破损检测的第一步是了解网衣的水下动态以分析相关数据。在数值模拟中，集中质量力学模型为经过验证的模型，可用于计算在洋流和海浪中柔性网箱和渔具的所受水动力荷载，更好地模拟其动态行为(Lee et al, 2008; Zhao et al, 2009、2013; Cifuentes et al, 2017; Jin et al, 2018; 崔勇等, 2019)。

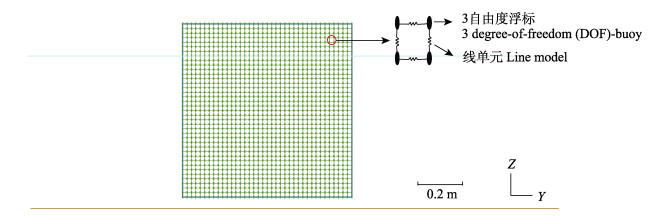
本研究使用商业软件OrcaFlex建立的网衣等效数值模型如图 4所示。该模型使用1521个3自由度浮标和2964条线单元来构建网衣模型。软件采用集中质量法对线单元的动力响应进行求解。所有线单元的附加质量系数固定为1.0，拖曳力系数设置为1.2 (Kim et al, 2020)。软件可以直接实现在给定时刻网衣发生破损的情况。整个模型的运动可描述为式(1):

$ M(p, a) + C(p, v) + K(p) = F(p, v, t) $

(1)

式中，M(p, a)为惯性力矩阵，C(p, v)为阻尼力矩阵，K(p)为刚度力矩阵，F(p, v, t)为外力矢量，即本研究中的水动力。符号p、v、a和t分别表示位置、速度、加速度和时间。水流和波浪对运动物体的水动力通过莫里森方程计算得到。对于圆柱形物体，单位长度的水动力可表示为：

$ {F_W} = {C_m}\rho \frac{{\pi {D^2}}}{4}\dot u - {C_a}\rho \frac{{\pi {D^2}}}{4}a + \frac{1}{2}\rho {C_d}D|u - v|(u - v) $

(2)

式中，C_m、$ {C_a} $、$ {C_d} $分别表示惯性、附加质量和拖曳力系数，其中，$ {C_m} = 1 + {C_a} $。D、$ \rho $分别为圆柱体外径和海水密度。$ \dot u $和u分别为流体水质点的加速度和速度。

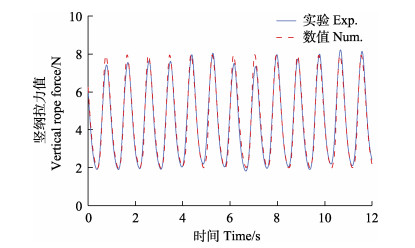
图 5所示为在规则波波高H为0.1 m、周期T为0.9 s时传感器数据与等效数值模拟所得仿真数据对比。由图 5可知，网衣在规则波的作用下，纲绳的受力历时曲线呈现波动变化。经计算，仿真数据与传感器数据的最大受力值与最小受力值的相对差异分别为3%和6%，数值模拟数据与物模实验数据吻合较好，表明建立的数值模型正确。

1.4 人工神经网络模型

开发人工神经网络的目的是从大数据中发现给定输入信号和输出信号之间的未知关系，建立起数字孪生体。Ojha等(2017)指出，有一层隐藏层的神经网络，隐藏层的神经元数量有限且具有S型激活函数，即可逼近任何函数，所以本研究使用图 6所示的3层神经网络结构。S型激活函数具体形式如下所示：

$ f(x) = \frac{1}{{1 + {e^{ - x}}}} $

(3)

对于神经元个数，本研究使用经验公式(Stathakis, 2009)来确定，公式如下所示：

$ m=2n+1 $

(4)

式中，n为输入层个数，m为隐藏层神经元个数，本神经网络模型共有4个输入，神经元个数设置为9个。

人工神经网络需要大量数据进行训练和测试。训练的数据由输入和目标输出成对组成。训练人工神经网络时，输入信号初始进入人工神经网络，人工神经网络将计算出的输出与目标进行对比，根据误差以及学习规则来修改连接的权重。本研究的人工神经网络采用比例共轭梯度法来更新权重，该方法具有所需计算内存小、稳定性高、收敛速度快的特点。由于是对网衣破损进行识别，故以Patternnet模式识别网络作为人工神经网络模型(Patternnet, 2021)。

表 1列出了用于构建数字孪生体的训练(标记为Tr)和测试(标记为Te)的海况，根据模型比尺1∶10进行缩放。本研究选择合适的环境条件，即有效波高(H_s)为0.1~0.3 m，谱峰周期(T_p)为1.0~3.0 s。训练样本数据由9个海况组成，测试样本数据由2个海况组成。采用JONSWAP谱作为波浪谱，水流流速与物模实验相同，为0.12 m/s，水流与波浪方向相同。

图 7为完整网衣及其破损时在水中某个时刻的平衡状态。网衣完整状态标记为(1, 0)，网衣发生破损时标记为(0, 1)。在数值模拟中，每次仿真的时间为450 s，时间步长为0.1 s。损坏发生在150 s时，其共有40 509组仿真数据作为训练集，9002组仿真数据以及5000组物理实验的传感数据作为测试集。该神经网络模型共有4个输入，分别为H_s、T_p、横纲、竖纲拉力的移动平均值，其移动窗口长度设置为1000。

图 8为数值模拟得到的网衣在有效波高H_s为0.1 m、谱峰周期T_p为1.0 s时的网衣横纲和竖纲的受力情况，前150 s是网衣完整时的受力时程曲线，后300 s是网衣发生破损之后的受力时程曲线。

在150 s时，随着网衣发生破损，网衣的密实度发生变化，而网衣受力与网衣的密实度有关(陈天华, 2017)，因此，横纲、竖纲的拉力传感信号的幅度和趋势也发生变化。类似地，网衣破损在其他海况都会导致拉力传感信号产生不同的幅度和趋势，从而可以通过机器学习算法检测网衣是否破损。

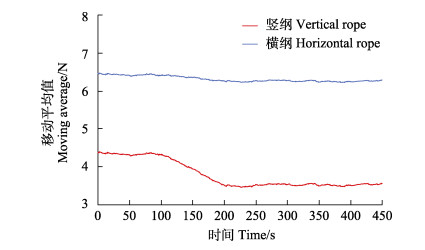
图 9为H_s=0.1 m、T_p=1.0 s时的横纲、竖纲拉力的移动平均值。对比图 8和图 9，经过移动平均值处理的信号具有了统计特征，网衣发生破损后，信号发生显著改变，其大大提高了神经网络的预测精度。

2 结果与分析

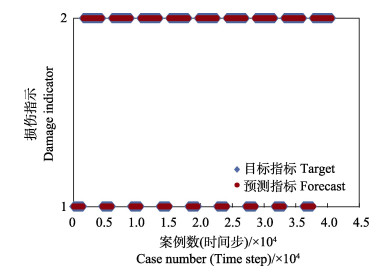
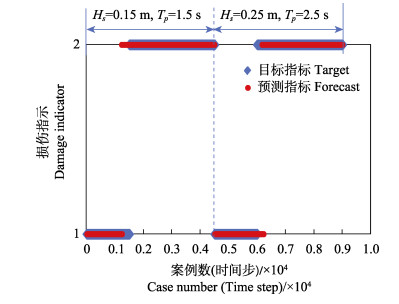
图 10为人工神经网络模型训练案例中目标指标和预测指标(标记为蓝色菱形和红色圆圈)的对比，如果红色圆圈和蓝色菱形重合，则表示预测准确，其纵坐标值1表示标签(1, 0) (网衣完整)，纵坐标值2表示标签(0, 1) (网衣发生破损)。图 11为人工神经网络模型对未用于训练的测试案例的预测对比。经过训练，该人工神经网络模型对训练集和测试集的预测准确度分别为99.21%和95.11%，其中，预测准确度采用以下公式计算：

$ 预测准确度(\%) {\text{ = }}\frac{m}{n} \times 100 $

(5)

式中，m为匹配的案例数，n为案例总数。参考有关利用数字孪生技术进行破损检测的文献(Ritto et al, 2021; Kim et al, 2020; Chung et al, 2020)可发现，均认为模型的识别准确率在90%以上即可判断该模型的识别准确度高，识别效果良好。

网衣受力与其网衣的密实度以及波浪大小等因素有关(陈鹿, 2015)。从以上结果来看，人工神经网络能根据不同的受力情况对网衣所处状态进行准确分类，且神经网络能对未用于训练的工况进行较好拟合，由此最终成功构建了可以用于网衣破损检测的数字孪生体。

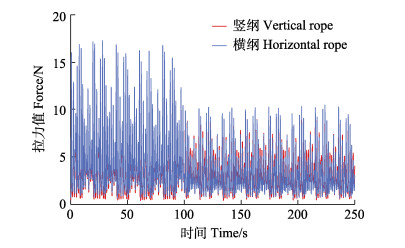
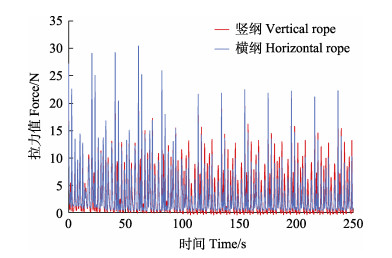
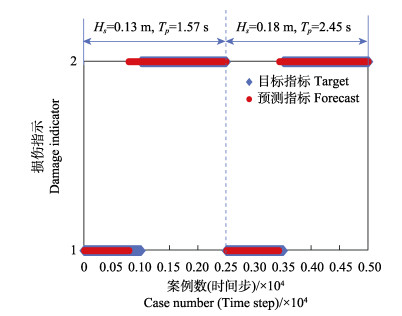
图 12为网衣物理模型在有效波高H_s为0.13 m、谱峰周期T_p为1.57 s时测得的拉力传感数据。图 13为网衣物理模型在有效波高H_s为0.18 m、谱峰周期T_p为2.45 s时测得的拉力传感数据。前100 s是网衣完整时的受力时程曲线，后150 s是网衣发生破损之后的受力时程曲线。将物理模型实验的传感信号作为测试案例，输入数字孪生体进行识别，数字孪生体对网衣的破损识别结果准确率达到94.32%(图 14)。

由图 14可知，数字孪生体对未用于训练的实测物理数据也能进行准确分类识别。如果将网衣的各种破损情况都进行大量仿真模拟并作为训练数据，那么数字孪生体的检测性能也将得到提高。另外，网衣的破损程度、传感器的数量、传感器的测量精度、人工神经网络隐藏层和神经元的设置也会对数字孪生体的识别精度造成影响。

3 结论

本研究介绍了用于平面渔网破损检测的数字孪生模型，该模型采用数值模拟和人工神经网络进行开发，通过识别横纲、竖纲的拉力传感器信号变化来检测网衣破损。人工神经网络的输入变量是有效波高H_s、谱峰周期T_p以及横纲、竖纲的拉力传感信号的移动平均值。人工神经网络的隐藏层为一层，神经元个数为9个。此次开发得到的数字孪生模型能对物理模型的传感数据进行网衣破损识别，准确率为94%。可见，数字孪生技术能准确检测到渔网的损坏，可以作为网衣破损检测的一种新方法。

本方法的研究对象是平面渔网，应用该方法对其他类型的网箱网衣进行检测时，存在传感器类型以及布置位置的差异。由于实际海域中的波流环境更加复杂，为提高渔网破损检测的准确率，如何在更加真实的海况下确定最佳神经元数量、传感器类型和数量是下一步的研究内容。