随着世界人口数量的不断增长，人们对于水产品的需求逐年上升。水产养殖作为可持续发展产业，为满足人们日益增长的水产品需求提供了新方向。联合国粮食及农业组织的报告显示，2020年全球鱼类产量约为2.14亿t，其中，来自水产养殖的部分约占总产量的49.2%，水产养殖业在全球水产品供应中具有重要地位(FAO, 2022)。网箱养殖作为水产养殖中的代表性养殖方式之一，在全球水产养殖业中应用广泛。在过去的几十年，浅水区域的网箱养殖呈现指数式增长，但由于近海区域空间有限，使得网箱养殖逐渐转移至深远海。尽管在开敞海域进行大规模网箱养殖可以有效地满足人们对于水产品的需求，并减少温室气体的排放，但仍存在一些限制因素。其中最主要的是，当养殖网箱安置在开敞海域时，结构会面临更加恶劣的海况。为了实现海洋养殖的安全生产，研究养殖网箱的抗风浪技术至关重要。

网衣系统作为养殖网箱的重要组成部分，其主要作用是维护养殖空间、保护养殖对象、防止养殖对象逃逸并抵御天敌侵袭。在波流场中，网衣系统会承受作用在养殖设施上的大部分荷载。相比于其他传统海洋结构物，网衣具有小尺度、高柔性的力学特点，在外力作用下网衣会产生大位移与大变形，导致养殖空间减小、养殖对象因拥挤而损伤的几率上升。同时，网衣的存在会改变养殖设施周围的波流场，影响结构中剩余饵料、养殖对象排泄物和水中溶解氧的分布。因此，系统掌握网衣的水动力特性尤为重要。

随着网箱养殖的不断发展，网箱结构形式更加丰富，网箱需要面临的环境荷载更为复杂。网衣作为养殖网箱的关键部分，其水动力特性值得深入探索。本文根据现有文献从网衣水动力荷载、网衣动态响应及网衣周围波流场3个方面展开综述。通过总结以上3个方面的热点问题，归纳今后研究网衣水动力特性的发展方向，以期为保障网箱结构安全、实现水产养殖的可持续发展提供参考。

网箱养殖在以往的几十年中发展迅速。从19世纪60年代至今，网箱养殖技术日益成熟并逐渐实现商业化(Sievers et al, 2021)。由于人们对水产品的需求日益增长且近海区域空间有限，网箱养殖逐渐转向深远海。相比于近海，网箱在开敞海域需要面临更恶劣的海况。网衣作为养殖网箱中最敏感的组成部分，需要承受复杂的环境荷载以及海洋生物的撕咬与碰撞。因此，掌握不同环境条件和结构尺度下网衣水动力荷载的变化规律，对保障养殖对象安全、优化网箱结构设计尤为重要。

网衣由网线编织而成，由于网线直径远小于海域中常见波长，属于小尺度构件。为了实现网衣水动力荷载的快速预测，人们通常采用经验公式计算荷载。求解网衣水动力荷载的经验公式可分为两类：

Morison模型：在求解过程中将网目目脚和结节分别假定为圆柱单元与球单元，通过Morison方程计算每根网线所受荷载，并求其矢量和近似代替作用在网衣上的水动力荷载(Morison, 1950)。Morison方程如下：

式中，${F_D}$为作用在网衣上的拖曳力，${F_I}$为作用在网衣上的惯性力，$\rho $为流体密度，${A_p}$为结构沿流体方向的投影面积，$U$对应流体速度，${C_D}$表示拖曳力系数，${C_M}$为惯性力系数，${C_M} = 1 + {C_m}$，${C_m}$为附加质量力系数，$\forall $为构件体积。

当网衣与流体产生相对运动时，Brebbia等(1981)建议对静态Morison进行改写：

式中，${U_R}$为结构与水质点之间的相对速度，$ {U_R} = $ $ U - R $，R为结构的速度。

面单元模型：该模型将整张网衣离散为若干相互连接的面单元，每个面单元覆盖实际网衣中的部分目脚和结节。网衣水动力荷载可通过下式计算：

式中，${C_L}$表示网衣升力系数。结合公式(1)~(4)可知，计算网衣水动力荷载的关键在于确定网衣水动力系数。

随着网衣材料、制造工艺的发展及网箱面临海况的多样化，网衣与流体之间的作用机理更为复杂，仅根据已有水动力系数估算网衣水动力荷载将导致较大误差。因此，通过模型试验或现场观测了解网衣的受力特点是必要的。Løland (1991)认为网衣水动力荷载与网衣的结构参数有关。然而，网衣结构参数的变化会改变网衣周围的流体属性，综合考虑网衣结构特征及流体属性的影响可提升网衣水动力荷载的预测精度(Dong et al, 2020)。此外，在养殖过程中，网衣会受到生物附着及鱼类的影响，二者均会改变网衣上的水动力荷载(He et al, 2018)。

为了全面了解网衣水动力荷载的变化特征，应分析多参数对网衣水动力荷载的影响。在以下内容中，将从网衣水动力系数及生物效应对网衣水动力荷载的影响两方面展开介绍。

国内外学者主要从水流和波浪条件下，通过物理模型试验研究网衣的水动力系数。根据求解网衣水动力荷载经验公式的类别，分别对Morison模型与面单元模型的水动力系数开展综述。

在水流条件下，网衣的水动力系数与雷诺数(Re)密切相关(Zhao et al, 2007a)。Kawakami (1964)通过Morison方程对均匀流作用下柔性网衣上的水动力荷载进行了计算，认为在水流条件下，Morison方程中仅保留拖曳力项。网衣的拖曳力系数取决于网衣密实度(S_n)和水流攻角(α)，相应参数的计算公式如下。

Fredheim(2005)提出了无结节菱形网目网衣密实度的计算公式：

式中，${d_w}$为网线直径，${l_w}$为目脚长度，$ {E_H} = $ $ {D_H}/2{N_H}{l_w} = \sin \alpha $，$ {E_V} = {D_V}/2{N_V}{l_w} = \cos \alpha $，${D_H}$和${D_V}$分别表示网衣宽度和网衣高度，${E_H}$和${E_V}$为水平方向和垂直方向的网目缩结系数，${N_H}$和${N_V}$分别为沿网衣宽度方向的网目数量，沿网衣高度方向的网目数量，2$\alpha $为网目张开角度，网衣基本属性如图 1所示。

图 1(Fig. 1)

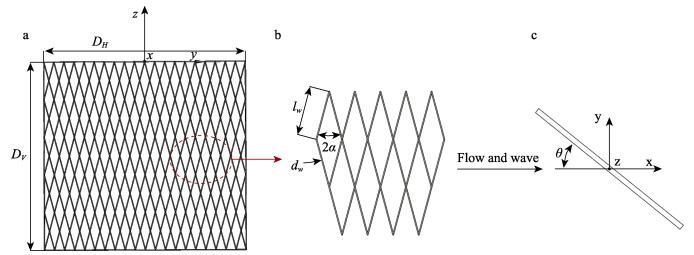
图 1 网衣的基本属性 Fig.1 Fundamental properties of the net a：无结节菱形网目的网衣；b：无结节菱形网目；c：来流攻角的定义 a: Knotless hexagon-mesh net; b: Hexagon-mesh; c: Definition of attack angle

当网衣结节直径较大时(${D_w}{\text{/}}{d_w}$=3.0~3.3，具体取值需对实际结节进行测量，${D_w}$为结节的直径)，计算网衣密实度的过程中需要考虑结节的面积(周应祺等, 2017)。对于菱形网目的有结节网衣，其密实度可通过以下公式计算：

当${E_H}$=${E_V}$=0.707时为方形网目。

Choo等(1971)对水流作用下缆绳上的水动力荷载进行了研究，并将其分为两部分：缆绳的法向荷载和切向荷载。对应公式如下：

式中，${C_{Dn}}$和${C_{Dt}}$分别为缆绳的法向和切向拖曳力系数。$\mu $对应流体粘性，$ s = - 0.077215665 + \ln (8/{\text{R}}{{\text{e}}_n}) $。$ {\text{R}}{{\text{e}}_n} $为基于法向速度的雷诺数。

DeCew等(2010)对公式(7)和(8)进行了拓展，得到了水流作用下无结节方形网目网衣的拖曳力系数。

当网衣结节直径较大时(${D_w}{\text{/}}{d_w}$=3.0~3.3，具体取值需对实际结节进行测量)，应考虑网衣结节的存在，一般可将结节近似为球体进行处理(周应祺等, 2017)。Fredheim(2003)建议结节部分的拖曳力系数应该在1.0~2.0之间。该系数的选取需要结合网衣结节的编织方法、直径以及雷诺数等因素。

在波浪条件下，网衣的水动力系数不仅与雷诺数有关，还与KC数有关(赵云鹏, 2007)。基于尺度分析原理得出作用在单位长度圆柱上的波浪力可通过以下公式进行表示：

式中，L为圆柱的总长度，k为圆柱表面的相对粗糙度，T为波浪周期，${U_m}$为水质点在一个波周期内的最大速度，D为圆柱直径。

联系Morison方程，不考虑时间因素的影响可得：

式中，${K_c} = ({U_m}T)/\nu $，$Re = ({U_m}D)/\nu $。

Zhao等(2008)基于最小二乘法计算了波浪作用下网衣的水动力系数，结果显示，当网衣的KC数在150~350范围内时，KC数对拖曳力系数的影响并不明显。同时发现，波浪作用下，拖曳力是网衣水动力荷载的主要部分，网衣上的惯性力数值很小，可以忽略。Zhao等(2009)通过公式(9)和(10)计算了波浪作用下网线的拖曳力系数，并通过试验进行验证。

Dong等(2019)研究了网片在Stokes二阶波作用下的水动力系数，并得出相应计算公式：

公式(11)、(12)的适用范围为$ 0.19 \leqslant {S_n} \leqslant 0.679 $，$ KC < 100 $。

Xu等(2021)分析了网片在极端波浪下荷载的变化规律，并给出了网衣水动力系数的计算公式：

式中，$ K{C^ * } = KC/(2.23S_n^2 - {S_n} + 0.282) $。若网衣材质为聚酰胺，公式(13)、(14)的适用范围为$ 0.19 \leqslant {S_n} \leqslant $ $ 0.652 $，$ 46 < K{C^ * } < 218 $。若网衣材质为钢，公式(13)、(14)的适用范围为$ 0.19 \leqslant {S_n} \leqslant 0.679 $，$ 47 < K{C^ * } < 363 $。

Balash等(2009)考虑了网衣密实度和雷诺数对网衣水动力系数的影响，提出了网衣拖曳力系数公式。

式中，$C_D^{cyl}$和$C_D^{sp}$分别代表圆柱形单元(目脚)和球形单元(网衣结节)的拖曳力系数。公式(15)的适用范围为0.051≤S_n≤0.235，$\text{Re} < 5 \times {10^3}$。

Kristiansen等(2012)考虑了来流攻角、网衣密实度和雷诺数对网衣水动力系数的影响，并总结了网衣拖曳力系数和升力系数公式：

式中，$\theta $为来流攻角，如图 1c所示。公式(16)、(17)的适用范围为${S_n} \leqslant 0.5$，$32 \leqslant \text{Re} \leqslant 10000$。

尽管网衣密实度和雷诺数分别为描述网衣结构特征及流体属性的无量纲参数，但在二者为常数时，网线直径、目脚长度和来流流速(${U_0}$)的变化也会改变网衣水动力荷载。为准确预测网衣受力，将以上参数综合考虑是必要的(Wang et al, 2022)。

在实际养殖中，海洋环境较为多变，网衣材料和编织工艺日益更新，采用已有的网衣水动力系数计算网衣水动力荷载会与实际产生较大差异。通过试验或者现场观测方法了解网衣水动力荷载的变化规律尤为重要。Dong等(2019)和Tsukrov等(2011)研究了水流或规则波作用下金属网衣的受力特点，认为受网线表面粗糙度影响，金属网衣(如：钢网衣、铜网衣)所受拖曳力要小于聚酰胺(尼龙)网衣。然而，在极端波浪(极限破碎波和崩破波)作用下，网线周围的流动状态极为复杂，波浪非线性越强，网线材料和结节类型对网衣水动力荷载的影响越小(Xu et al, 2021)。

根据上述讨论可知，网衣结构参数或流动属性的变化均会改变网衣水动力荷载。但上述公式仅适用于无生物附着网衣水动力系数的计算。然而，在实际养殖工程中，网衣会受到生物效应(附着生物和养殖对象)的影响，这会导致网衣水动力荷载的显著变化。

在网箱养殖过程中，网衣会受到生物效应的影响，如附着生物及养殖鱼类的影响。为了解生物效应对网衣水动力荷载变化规律的影响，本节将从生物附着和养殖鱼类两方面分别展开介绍。

生物附着是海洋生物的堆积，会导致网目堵塞，网衣水动力荷载显著增加(Fitridge et al, 2012)。网衣上的附着生物种类繁多，其物理特性及分布形式均会改变网衣水动力荷载。为研究生物附着的影响，国内外学者通常采用现场测量和物理模型试验方法。Swift等(2006)对海洋生物附着平面网衣的受力特性进行了研究，并通过实验室模型试验和现场测量的方式对水流作用下不同附着程度网衣的受力进行了测量。Lader等(2015)采用模型试验的方法对附着有水螅虫的单根网线在水流作用下的受力特性的分析结果表明，网线的受力与附着生物(水螅虫)的长度、生长时间、网线雷诺数密切相关。Gansel等(2015)利用物理模型试验，针对水螅虫这种附着物对水流作用下平面网衣的受力特性进行了分析，获得了网衣受力与生物附着后的网衣密实度之间的函数关系。Bi等(2018a)开展了现场挂片试验，并通过控制网片的浸没水深与时长，获得了具有不同生物附着程度的网衣。在波流水槽中开展了一系列物理模型试验，测得了不同水流流速下，不同附着程度网衣所受拖曳力及相应的拖曳力系数。研究表明，附着物可使得网衣所受水流力增加至原来的10倍以上。此外，不同的网线编制工艺会改变网线的表面结构与纹理，进而影响生物附着。Dos Santos等(2020)认为复丝网线相较于单丝网线，其表面更为粗糙，易于海洋生物附着，增加网衣水动力荷载。因此，在实际养殖过程中应注意及时对网衣进行清洗或更换(Bi et al, 2020b)。

网衣周围养殖鱼类的游动会影响网衣附近的流场，改变网衣水动力荷载。当前主要采用现场观测和试验方法研究养殖对象对网衣水动力荷载的影响。Bi等(2020a)研究了鲫鱼幼苗对重力式网箱所受拖曳力的影响，认为当鱼类迎流游动且不与网衣接触时，鱼类存在对网箱所受拖曳力的影响很小。当流速过大时，鱼类与网箱接触会导致网衣局部密实度增大，网衣受力显著增加(He et al, 2018)。Park等(2022)分析了鱼群环游对网箱受力的影响，认为鱼群环游会减小网箱受力。这是因为鱼群环游会产生离心力，影响水流速度，改变水流方向，并增加水的混合。因此，网箱中的湍流强度增加降低了网箱背流侧网衣所受拖曳力。

网箱养殖过程中，网衣在波浪和水流作用下会产生变形，导致网箱养殖体积减小，威胁网箱安全和养殖对象的福利。因此，研究如何减少外荷载作用下网衣的变形，对保障网箱的养殖空间具有重要意义。本节主要对数值模拟方法进行介绍。根据计算原理可将数值模拟方法大致分为两类：有限元方法和计算流体力学方法(computational fluid dynamics, CFD)。

根据单元的类型，通过有限元方法模拟网衣系统的数值模型大致可分为4种(图 2)：三角形单元模型(Priour et al, 1999)、桁架模型(Tsukrov et al, 2003)、集中质量模型(Huang et al, 2006; Li et al, 2006a)和板网单元模型(Lader et al, 2001)。

图 1(Fig. 1)

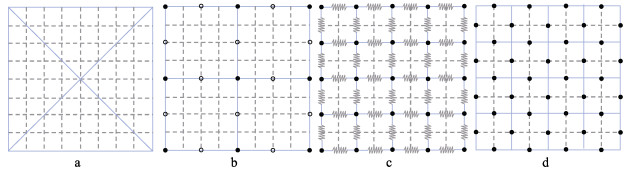
图 2 4种有限元模型单元示意图 Fig.2 Four types of finite element model cells a：三角形单元，单元通过实线表示(Priour et al, 1999)；b：桁架单元，通过实线进行代替(Tsukrov et al, 2003)；c：集中质量模型(Li et al, 2006)；d：板网单元模型(Lader et al, 2001) a: Triangular element, represented by solid lines, reproduced from Priour et al (1999); b: Truss element, represented by solid lines, reproduced from Tsukrov et al (2003); c: Lumped-mass element, reproduced from HUANG2006">Li et al (2006); d: Panel net element model, reproduced from Lader et al (2001).

Priour等(1999)提出了三角形单元模型，为了将网衣离散，忽略了单元侧边是否与网线平行。该模型假设每个三角形单元的伸长量和弹性模量为定值。如图 2a所示，网衣通过已定义节点连接成的三角形单元建模，这些节点用于确定网衣的平衡位置。由于网线与结节被视为圆柱和球体，所以它们可以通过相应的单元进行代替。在求解过程中，通过Newton-Raphson方法对每个时间步网衣的平衡位置进行计算。

三角形单元的边不需要与网线平行，且可将一个单元细化为多个单元。基于上述特点，小尺寸三角形单元可以用来模拟网衣高度变形的区域，其余部分可通过大尺寸三角形单元进行描述。在模拟过程中，一个三角形单元可以表示真实网衣的多个网目。因此，三角形单元模型是一种网衣群化的方法(Li et al, 2006)。

桁架模型假设网线之间没有相互作用。当网衣通过桁架模型进行模拟时，将网衣离散为独立的网线和结节。每个桁架单元都有一个中心节点，并且单元可以在压力作用下屈曲。网衣在每一时间步的平衡位置可通过迭代算法进行计算，例如：Newton-Raphson迭代算法。在模拟过程中，可通过一个桁架单元代替几根真实网线。为了减小单元数量，改善计算效率，Tsukrov等(2003)基于桁架单元提出了一致性网衣模型。图 2b显示了一致性网衣单元模型中具有代表性的等效桁架单元。网衣水动力荷载可通过Morison方程计算(Fredheim et al, 2001)。与此同时，桁架模型可以对网衣结构的细节进行考虑。目前，桁架模型已广泛应用于网箱水动力特性研究。

集中质量模型是将网衣上的所有结节与每个网目的目脚中点都定义为集中质量点，并通过无质量弹簧进行连接，具体如图 2c所示。作用在网衣上的水动力荷载可以通过Morison方程进行计算。通过五阶Runge-Kutta方法求解运动微分方程。为了改善计算效率，可采用网衣群化的方法，将多个真实网目由具有相同几何形状和物理特性(如投影面积和水动力系数)的等效网目表示。目前，网衣群化方法已广泛用于研究水产养殖网箱的水动力特性(Zhao et al, 2007b; Xu et al, 2012; Hou et al, 2017; Yang et al, 2020)。

通过集中质量法可以对网箱变形及其运动响应进行求解。Li等(2006)基于集中质量法，提出了水流作用下三维网衣的动力学模型。在不同流速下，计算了配有不同重量沉子重力式网箱的网衣变形和水动力荷载。Zhao等(2007b)将刚体运动学和集中质量法结合，建立了重力式网箱的数值模型。计算了重力式网箱在纯流、纯波和波流联合作用下的运动、网衣变形和系泊力。Chen等(2009)建立了波浪中带网格系泊系统的网箱数值模型。随着网格下潜深度的增加，浮架的水平运动幅度明显减小，而垂直运动幅度变化不大。Dong等(2010)分析了重力式网箱在波浪中的水动力响应，发现系泊力随着波浪频率的增加而减小。Zhao等(2010)计算了重力式网箱在漂浮和淹没状态下的系泊力和网箱运动。结果表明，网箱淹没后，系泊力与网箱运动响应均明显减小。Xu等(2013)建立了网箱和网格系泊系统在波浪和水流条件下的数值模型。发现在漂浮状态下，锚绳上的最大张力随着波陡的增加而增加。在淹没条件下，波陡对锚绳上的最大张力没有显著影响。Zhao等(2013a)建立了箱形网箱的数学模型，模拟了箱形网在纯波浪和水流中的系泊力和运动响应。在纯波浪和水流作用下，圆柱形网箱比箱形网箱更稳定。

板网单元模型是将网衣分为多个面板单元，相邻面单元通过节点连接，具体如图 2d所示。为了提高计算效率，可通过一个虚拟面板单元代替多个真实网目。模拟过程中，节点可进行三维运动。面板单元的结构特征与非线性弹簧相类似。作用在任意一个网板单元上的力会均匀分布到相邻单元节点上，同时质量也均匀分布在对应节点上。

对比以上4种有限元方法可知，四者的主要区别在于离散单元类型不同。三角形和板网单元模型需要将网衣离散为小尺寸的面单元，而集中质量和桁架单元模型则是将网衣离散为质量点与杆单元。通过上述有限元方法均可考虑网衣的运动与变形，并可采用网目群化减少计算量。然而，上述模型仅通过流速衰减系数来近似考虑网衣周围的流速变化。由于网箱形状、数量和网箱间距的影响，网箱内部及网箱之间的流速分布并不均匀(Bi et al, 2018b)。为准确描述网衣的动态响应，需要考虑网衣周围的实际流场变化。

与有限元模拟方法不同，通过计算流体力学方法获取作用在网衣上的水动力荷载时必须考虑流体粘性的影响，且控制方程为Navier-Stokes方程。一般通过离散方法，如有限体积法(finite volume method, FVM)，对控制方程进行离散。通过求解离散化的控制方程，可以得到流体的速度场与压力场。

为了提高计算效率，一般采用多孔介质模型模拟网衣。多孔介质模型是一个假想的模型，它在多孔介质区域结合了一个根据经验假设为主的流动阻力，通过合理设置多孔介质系数，使得多孔介质具有与网衣相同的阻流效果，得到网衣周围的流场情况(Bi et al, 2014a; Zhao et al, 2013a)。在计算过程中，通过二阶精度的有限体积方法对雷诺平均的Navier-Stokes (RANS)方程离散。采用分离式解法中的压力修正法计算速度场与压力场(Patankar et al, 1983)，并通过湍流模型考虑其背后的湍流机理。目前而言，学者们选取的湍流模型都是基于Boussinesq假设的湍流模型，如k-Epsilon、k-Omega等(Launder et al, 1983)。

多孔介质模型的设置关键在于多孔介质系数的选取，该系数可通过多种方法确定。Patankar等(1983)使用归一化的最小平方误差来寻找最佳多孔介质系数。Zhao等(2013c)根据试验数据，通过最小二乘法获取了网衣多孔介质系数。尽管通过多孔介质模型可以考虑网衣周围的流场特性，但是该方法无法精细考虑网线周围的流场变化以及网线的运动(Martin et al, 2020)。

为了解决计算流体力学方法求解网衣水动力问题存在的不足，学者们提出有限元方法和计算流体力学相结合的流固耦合模型。通过多孔介质模型考虑网衣周围的流场，并采用有限元模型对网衣变形进行模拟。Bi等(2014b)将集中质量法与多孔介质模型相结合，建立了水流作用下柔性网衣的数值模型。与试验结果相比，该模型可以近似地模拟网衣变形及网衣周围的流场特性。Chen等(2017)对上述模型进行完善，考虑了网衣与流体间的相互作用，可模拟水流作用下柔性网衣的变形。在此基础上，通过刚体运动求解器对浮架的运动响应进行计算，并与上述流固耦合模型相结合，实现了波浪和水流作用下重力式网箱的运动响应的近似估计(Chen et al, 2018)。Tang等(2017)基于计算流体力学方法，建立了拖网的三维数值模型，并通过大变形非线性结构模型(LDNS)对拖网在水流中的结构变形进行了分析。Martin等(2020)开发了一种拉格朗日方法，用在基于浸没边界法的欧拉流体模型中，对网衣在波浪作用下的运动响应进行了模拟。

总的来说，计算流体力学方法可通过多孔介质模型考虑网衣周围的流场，但在处理网线周围的精细化流场时存在不足。将有限元方法与计算流体力学相结合的流固耦合模型，既有效地考虑了网衣变形，又兼顾了流场特性的分析，但模型网格数量一般在千万量级，导致计算效率较低。

网衣周围流场和波浪场的变化会直接影响养殖网箱内外的物质运输和鱼类游动。当流速过低时，网箱内残余饵料和鱼类排泄物等有害物质无法及时从设施中清除，致网箱内水质变差，影响鱼类健康(Zhao et al, 2013a)。相反，过高的流速会造成鱼类不适，不利于它们的存活与生长。同时，极端波浪与网箱相互作用会产生越浪，导致鱼类逃逸(Bi et al, 2014a)。因此，分析渔网周围的流场和波浪场是确保鱼类福利、减少经济损失的有效途径。为系统了解网衣周围的波流场特性，改进养殖网箱的设计与管理，本节从网衣的尾流效应、流场和波浪场三方面进行综述。

尾流效应是网衣流场分析中的一个重要且复杂的机理。网衣下游的尾流区是流速扰动区域(通常是湍流)(Zhao et al, 2013a)。研究网箱网衣系统的尾流效应时，可按照影响范围，将网衣的尾流效应分为3种：网线之间、网衣之间、网箱之间的尾流效应(图 3)。

图 1(Fig. 1)

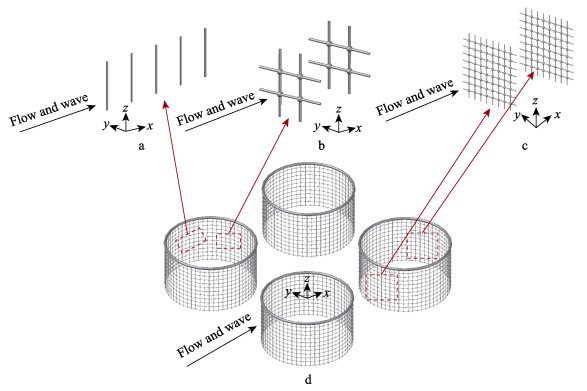
图 3 网衣系统的尾流效应 Fig.3 Wake effect of the net system a：网线；b：网目；c：网衣；d：网箱 a: Twines, b: Mesh, c: Nets, d: Net cages

网线之间的尾流效应存在于网目目脚之间。由于目脚结构可简化为圆柱结构，根据这一假设，可采用Blevins(1990)提出二维圆柱尾流流速计算公式考虑网线下游的流速衰减。

式中，${U_{down, t}}$为网线下游流速。

Fredheim(2005)在Blevins(1990)研究基础上考虑多个圆柱对流速衰减的影响，并提出相应计算公式：

式中，${U_i}$为圆柱i处时间平均的流速，$({x_i}, {y_i})$对应圆柱i的坐标(其中，i=1, 2, 3 … N)。参考公式(18)和(19)可知，当网线下游的位置与上游网线距离远大于网线直径时，网线之间的尾流效应几乎可以忽略。

上述研究所针对的是单个网线之间的尾流效应。在养殖工程中，网衣通常是由2个交叉网线组成的十字型单元构成(Osaka et al, 1983)。同时，杆件相互垂直排布产生的交互作用使得十字型单元周围产生了明显的“二次流”(Fox, 1991)。因此，了解圆柱十字单元的尾流效应有利于理解网衣周围的流态。近年来，随着计算机计算性能的提升，学者们通过CFD对圆柱十字单元周围的流场展开了研究，并分析了网目形状、雷诺数、密实度对单元尾流的影响(Bi et al, 2017a; Tang et al, 2021)。

尽管网衣是由网线和圆柱十字型单元组成，但网衣的尾流效应并非上述单元尾流效应的叠加(Wang et al, 2021)。因此，需要对网衣的尾流特性开展研究。

网衣之间的尾流效应通常表示为同一网箱中网衣之间的相互作用。对于重力式网箱而言，几乎一半的网衣都会受到网衣之间尾流效应的影响。在研究过程中，一般通过流速衰减因子(r)考虑网衣之间的尾流效应。位于尾流区域中的网衣对应的流速可通过下式计算：

式中，$ {U_{{\text{up, n}}}} $、$ {U_{{\text{down, n}}}} $为网衣上、下游的流速，r为流速衰减因子。现有研究中的流速衰减因子见表 1。

表 1(Tab.1)

表 1 网衣下游流速衰减因子 Tab.1 Flow reduction factors of the nets 模型Model 流速衰减因子Flow reduction factors 网衣密实度Sn 雷诺数Re 参考文献Reference R1 0.69 0.128~0.223 170~1 438 Zhan et al, 2006 R2 1~0.46CD 0.13~0.32 1 400~1 800 He et al, 2018; Kristiansen et al, 2015; Shen et al, 2018 R3 0.85 0.20~0.22 18~60 Huang et al, 2006; Xu et al, 2013 R4 0.8 0.225 72~936 Li et al, 2006; Zhao et al, 2007a R5 0.873 0.081~0.238 89.6~1 638 DeCew et al, 2010

表 1 网衣下游流速衰减因子 Tab.1 Flow reduction factors of the nets

根据现有的网衣下游流速衰减因子计算公式可知，现有模型通常考虑的是网衣密实度及雷诺数的影响。对于其他参数(例如来流方向、网线直径、材料、结节类型等)对流速衰减的影响并未予以分析。因此，将来的研究应关注多参数与网衣尾流效应的关系。

网箱之间的尾流效应通常为网箱阵列中网箱之间的相互影响。由于网衣对水流的阻碍作用，网箱阵列中位于下游的网箱周围流速要明显高于上游网箱。不同于网线及网衣之间的尾流效应，网箱与网箱间的相互作用更为复杂(Lader et al, 2005)。由于网箱形状、数量、网箱间距的影响，网箱之间的流速分布十分复杂(Bi et al, 2018b)。因此，通过单一的流速衰减因子难以准确描绘网箱间复杂的流场变化。

总的来说，研究网箱的尾流效应是了解网箱周围流场的关键点之一。所以，结合现有研究并考虑新型网箱结构及多参数影响，分析高精度流场是进一步掌握网箱尾流特性、推动网箱养殖发展的基础。

目前，学者们通过试验和数值模拟方法对网衣周围的流场进行了研究。Bi等(2013)进行了一系列物理模型试验，以研究在水流中网衣下游的流速衰减。通过粒子图像测速(PIV)技术和声学多普勒测速仪(ADV)获得了网衣下游的流速分布。研究发现，网衣下游流速明显降低，且降低幅度随网衣密实度的增加而增大。随着网板与垂直方向之间倾角的增大，流速的衰减逐渐增大。Zhao等(2013b)通过计算流体力学方法，建立了网衣的三维数值模型，并模拟了水流作用下网衣周围的流场，结果显示，当网衣倾角大于45°时，网衣周围流场会产生明显变化。随着网衣数量沿水流方向增加，下游流速会逐渐衰减。Zhao等(2013c)建立了重力式网箱的三维数值模型，并模拟了水流作用下网箱周围的流场。研究表明，当2个网箱沿水流方向布置时，网箱间距的变化不会明显影响网箱内部的流速衰减幅度。当网箱沿水流方向逐渐增加时，下游流速衰减幅度逐渐增大，但下游网箱的存在不会影响上游网箱内部的流场。Bi等(2014a)将有限元方法与计算流体力学方法相结合，建立了水流作用下柔性网衣的数值模型，并研究了单片网衣和两片网衣周围的流场。结果显示，由于网衣孔隙率较大，使得单片柔性网衣周围的水流方向变化并不明显。与单片网衣相比，两片网衣周围水流流向变化更为明显。同时，网衣遮蔽效应随着沿水流方向网衣数量的增加而增大。Liu等(2021)研究了半潜式渔场平台的流场特性，数据显示，网衣的存在扩大了平台内部的低流速区域，并且随着网衣密实度的增加，平台内部的流速衰减越明显。Bi等(2020a)通过试验方法研究了养殖鱼群对网箱内外流场的影响，结果显示，鱼类的运动增大了网箱内部及网箱下游的流场变化，流体的湍流强度随着鱼类养殖密度的增大而增大。

由于网衣的存在对波浪的传播具有阻挡和耗散作用，因此，需要对网衣周围的波浪场展开研究。Zhao等(2014)研究了网衣与波浪间的相互作用，发现网衣密实度的变化对波的传播几乎没有影响。随着波高的增加，波浪透射系数保持不变。波浪透射系数随波长的增加而增加。Bi等(2015)通过物理模型试验研究了波浪作用下网箱的阻尼效应，发现受网箱影响，网箱内部及其周围的波浪场有明显的三维效应。对于网箱群组而言，随着波周期增大，波浪透射系数逐渐增大，且网箱数量越多，波浪透射系数增加越明显。网箱对波浪的阻尼效应随着网箱数目的增长而增长。与网箱下游相比，网箱内部的波浪透射系数更大。网箱下游的波浪透射系数随着网箱间距的增大而减小。Zhao等(2016)研究了直列式网箱群组在波浪作用下，网箱内部及其周围的波浪场，结果显示，随着网箱数量沿波浪传播方向逐渐增加，网箱下游的波浪透射系数逐渐减小。

在实际养殖过程中，网衣上的附着生物及网箱内的养殖对象均会对网衣周围的波流场产生影响。首先，附着生物会导致网目堵塞，降低网箱内外水交换速率、增加网箱内部及下游的流速衰减幅度(Gansel et al, 2012)。毕春伟(2016)建立多孔介质模型模拟生物附着网衣，对水流作用下原型尺度的网箱内外流场特性开展了研究。与无附着物的工况相比，网箱内部和下游流速的衰减幅度随着网衣被附着程度的增加而增大，网箱内部流场分布的不均匀性也会逐渐增大。在此基础上，Bi等(2018b)对潮流作用下网箱阵列(以2×4的网箱阵列为例)流场特性进行了模拟，总体而言，生物附着程度越大，对网箱周围潮流场的影响越明显。与未考虑生物附着影响的结果相比较，附着物的存在使得网箱内外波浪场发生明显改变。网衣被附着程度越严重，网箱阵列对波浪场的影响也就越大。波浪传播穿过网箱阵列后，由于网箱及附着物的阻尼作用，波峰和波谷都有所消减(Bi et al, 2017b)。其次，网箱内养殖鱼类的存在与游动会减小水流流速并改变水流方向(Klebert et al, 2013)。鱼类游动过程中，鱼体和鱼鳍的摆动会促进鱼类背后局部射流和漩涡的产生，从而影响网箱内部及周围的流场(Masaló et al, 2016)。由于单条鱼类对流场影响的程度相对有限，人们通常研究鱼群对网衣周围流场的作用。一些鱼类倾向于形成一个圆环状的鱼群，并以环形模式游泳。为了保持环形模式，鱼类必然会有朝向网箱中心的向心力使得网箱表面的水体向中间汇聚。然而，这种向心力与网箱外部的水体平衡，导致水流方向发生偏转(Gansel et al, 2014)。

研究网衣系统的水动力特性对于养殖设施的结构设计与安全评估至关重要。本综述介绍了网衣水动力特性的研究进展，为柔性网衣结构水动力特性研究的发展提供建议和对策。

为了确保网箱养殖的结构安全，准确预测网衣上的水动力荷载一直是人们关注的焦点。根据现有研究，求解网衣水动力荷载的主要方法是通过经验公式计算，其中，水动力系数的选取决定了计算结果的准确性。到目前为止，国内外学者拟合的水动力系数经验公式主要考虑了网衣结构参数、流体流动属性和生物效应的影响。但这些公式所考虑的影响因素是有限的。随着网衣材料和编织工艺的日益更新，网衣基本参数的变化会影响网衣的力学特征(Zhou et al, 2015)。在复杂环境条件下(如：孤立波、聚焦波和极限破碎波)，网衣水动力荷载会产生强非线性(Xu et al, 2021)。同时，柔性网衣在水流和波浪作用下会产生变形，增加网衣水动力荷载的计算难度。多类附着生物及养殖对象对网衣水动力荷载产生的影响也应予以考虑。

在今后的研究工作中，可以通过物理模型试验建立网衣水动力系数的数据库。同时，采用智能化算法，如数字孪生技术等，构建预测模型，生成多种因素与网衣水动力系数的映射关系(连栗楷等, 2022)。此外，数据库与算法应实时更新，用以提升网衣水动力荷载的计算精度。

对于网衣动态响应研究的数值方法主要有两种，有限元方法和计算流体力学方法。在实际应用过程中，必须衡量每种方法的优缺点，使用现有的有限元模型求解网衣动态响应时，可以通过网目群化方法提升计算效率，但有限元模型通常采用流速衰减系数近似考虑网衣周围的流速变化，这会导致计算结果与网衣实际变形产生差异。在计算流体力学方法中，可以通过多孔介质模型对网衣周围的波流场进行模拟，并考虑生物附着对网衣水动力特性的影响，但该模型无法精细捕捉网线周围的流场。尽管将有限元方法与计算流体力学方法相结合的流固耦合模型极大地推进了网衣的数值模拟进程，但通过该方法建立的数值模型网格一般在千万量级，导致计算效率较低。

在未来研究中，需要对柔性网衣的流固耦合问题开展深入研究，重点关注网衣与流体之间的双向耦合、探索直接数值模拟方法。在考虑计算精度的同时，应选取适宜的算法，如浸没边界法等，并开展并行计算方法的开发以提升计算效率。

网衣周围的波流场决定了网箱内外的水交换速率，直接影响了水中营养物质、溶解氧、废物等的分布。然而，当前的大多数研究主要关注于网衣周围的流场。对于深远海网箱养殖，网箱需要面对恶劣的波浪条件，所以了解网衣周围的波浪场是促进网箱养殖发展的重要支撑。同时，为抵抗极端海况，近年来大型自动化钢结构养殖平台得到了越来越多的关注，平台框架与网衣间的交互作用会显著改变周围的流场与波浪场，分析复杂结构引起的特殊流场现象是未来需要面临的一大挑战。此外，对于鱼群效应和附着生物带来的波流场变化也应持续研究(Bi et al, 2020a)。

随着水产养殖的不断发展，了解极端波况下网衣周围的波浪场变化是推广网箱养殖适用范围的基础。同时，在后续的研究中，考虑生物附着种类、附着密度、养殖鱼种、鱼类尺寸、数量、鱼群游动速度和游动状态等因素对网箱内流场的影响更利于监测鱼类的健康、降低鱼类患病风险、保证网箱养殖的可持续发展。