渔业资源调查是获取渔业资源评估和管理数据的来源，其精度对于生物多样性保护至关重要，影响着生物多样性保护措施的有效性(Chih, 2010; Xu et al, 2015a; 韩青鹏等, 2019)。然而，在海洋中开展渔业资源调查，成本高、代价大，且受到现场情况制约，因此，调查前周密的设计是确保生物多样性数据质量、实现调查效益最大化的前提(孟新翔等, 2019; 张国晟等, 2021b)。样本量的增加能提高结果的准确性(赵静等, 2014; 王晶等, 2017; 王家启等, 2017、2018; 孟新翔等, 2019)，但是，随着样本量的增加，调查成本也随之增加，同时，可能加剧对海洋环境以及群落的影响(Xu et al, 2015b; 孟新翔等, 2019; Nilsson et al, 2019; Trenkel et al, 2019)。最佳的采样设计能够在一定管理目标和预算下，获得精度最佳的样本数据(王家启等, 2017)。因此，采样设计应在样本量与调查精度之间寻求平衡，在预定管理目标和预算下准确性最高。

渔业资源调查站位优化被广泛认为是提高渔业资源调查精度的有效方法(Trenkel et al, 2019)，近年来，国内外已开展了多项相关研究(Liu et al, 2009; 唐政等, 2019; 张国晟等, 2021a; 程文等, 2022; 李迎冬等, 2022)。在渔业资源调查中，随机抽样、分层抽样及系统抽样是常见的采样方法(赵静等, 2014; 韩青鹏等, 2019)。近年来的研究表明，分层抽样具有较高的精确度，常用于渔业资源调查站位优化(Simmonds et al, 1996; Cabral et al, 2004; Drake, 2007; 赵静等, 2014; Xu et al, 2015b; 韩青鹏等, 2019)。然而，目前的研究多侧重于分层或样本分配的优化，较少关注同时优化分层和样本分配的方法。在这一背景下，基于遗传算法的R语言数据包SamplingStrata提供了一种有效应对多变量情境下的采样设计优化问题的解决方案(Barcaroli, 2014)。本数据包可在多个分层变量和多个目标变量的情况下确定满足精度约束的最佳分层、最佳样本量以及样本分配。该数据包采用每个目标变量的最大变异系数(coefficient of variation, CV)来表示精度要求(Barcaroli, 2014; Oyafuso et al, 2021)。该值反映了目标变量的样本估计方差相对于其均值的大小。CV值较高表示变量的值在均值周围波动较大，具有较高的变异性，而CV值较低表示变量的值波动相对较小，变异性较低。目前，该方法已成功应用于意大利国家统计局的多个调查项目(Ballin et al, 2013、2016)，同时，一些学者还将该方法应用于阿拉斯加海湾多物种渔业底拖网调查及农业部门的抽样调查中，结果显示，SamplingStrata方法能有效降低样本需求量(Catanese et al, 2017; Oyafuso et al, 2021)。

本研究以广东省茂名海域为例，旨在同时优化分层和样本分配，以评价茂名海域渔业资源调查中生物多样性调查所需最佳站位数量，并提高分层的效能。通过这一优化，以期为今后海洋生物多样性调查站位设计提供参考。

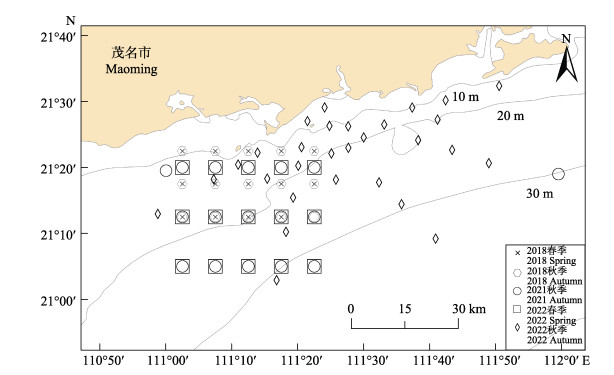
1 材料与方法 1.1 数据来源

数据来源于2018年3月和10月、2021年9月、2022年4月和11月茂名海域底拖网渔业资源调查，对应的调查站位分别为14、15、17、15和29个(图 1)。调查海域水深范围为9.8~39 m。利用单船底拖网进行调查，网囊网目长度为25 mm。每个站拖网时间约为40 min，拖速约为3 kn，受海况等因素的影响，各站位的实际拖速、拖网时间有偏差，因此，在数据分析前先进行标准化处理，即统一换算成拖速3 nmile/h情况下每小时的渔获量(kg/h)。现场调查采样和分析参照《海洋调查规范–第6部分：海洋生物调查》(GB/T 12763.6-2007)。

1.2 数据分析 1.2.1 生物多样性指数

本研究以茂名海域底拖网所捕获的生物多样性指数和物种数为目标变量，对茂名海域渔业资源底拖网调查采样站点数量进行优化。生物多样性研究选用香农–威纳多样性指数(Shannon-Wiener diversity index, H′)、Margalef丰富度指数(D)和Pielou均匀度指数(J′)(Shannon et al, 1963; Margalef, 1958; Pielou, 1966)：

香农–威纳多样性指数：

$ H' = - \sum\limits_{i = 1}^S {({P_i}{\text{lo}}{{\text{g}}_2}{P_i})} $

(1)

Margalef种类丰富度指数：

$ D = {{(S - 1)} \mathord{\left/ {\vphantom {{(S - 1)} {{{\log }_2}}}} \right. } {{{\log }_2}}}N $

(2)

Pielou均匀度指数：

$ J^\prime {\text{ = }}{{H^\prime } \mathord{\left/ {\vphantom {{H^\prime } {{{\log }_{\text{2}}}}}} \right. } {{{\log }_{\text{2}}}}}S $

(3)

式中，S为物种数，N为全部种的个体总数，P_i为第i个物种的多度比例。

1.2.2 站位优化设计

本研究旨在利用R语言中的SamplingStrata包，通过分层抽样来优化站位设计。在使用该数据包进行操作之前，首先需要构建具有分层结构的数据框。构建数据框前，必须明确定义分层变量和目标变量，并预先设定目标变量的精度要求[用每个目标变量的最大变异系数(CV)来表示]。分层变量的选择应基于它们与目标变量之间的相关性。选择与目标变量最相关的分层变量可以提高样本的代表性。

$ {\text{CV}}({Y_g}) = \frac{{\sqrt {{\text{Var}}({Y_g})} }}{{E({Y_g})}} $

(4)

$ {\text{Var}}({Y_g}) = \sum\limits_{h = 1}^H {{N_h}^2} \left({1 - \frac{{{n_h}}}{{{N_h}}}} \right) \cdot \frac{{S_{h, g}^2}}{{{n_h}}} $

(5)

式中，n_h为h层的样本大小；Y_g为不同的目标变量；Var(Y_g)为变量Y_g的样本估计的方差；E(Y_g)为变量Y_g的样本估计的均值；N_h和S_h,g² (其中，h=1, ⋯, H；g=1, ⋯, G)分别为h层抽样单位的数量和每个层次h中的G个不同目标变量Y的方差。

在选择分层策略后，将总体数据分成不同的层次，并利用SamplingStrata包中的“optimStrata”函数进行优化。该函数基于遗传算法实现分层抽样设计优化，本研究使用了“atomic”方法执行这一优化步骤(其中，分层变量是分类型变量，而连续变量则经过聚类k-means算法进行分类处理)。在默认情况下，每次迭代的解数为20，进行50次迭代(iter=50, pops= 20)。若最佳迭代曲线的尾部趋向于与x轴平行，则不增加迭代次数；相反则增加迭代次数，直至曲线尾部趋向于平行于x轴(Barcaroli, 2014)。最终，通过遗传迭代算法，确定在不同精度要求下的最佳分层设计和所需的样本数量。

在优化完成后，利用SamplingStrata包中的“selectSample”函数从优化后的最佳分层设计中选择样本。本研究分别以环境数据(水深、溶解氧、水温、pH和盐度)和水深作为分层变量，以香农–威纳多样性指数(H′)、Margalef丰富度指数(D)、Pielou均匀度指数(J′)和物种数作为目标变量。依次对目标变量设置CV为0.2、0.15、0.1、0.05、0.04、0.03、0.02、0.01，最初设定每次迭代的解数为20，迭代50次(iter=50, pops=20)。最终，从优化后的分层设计中选择样本，并计算该样本的相对误差(曾繁慧等, 2021)。

$ {E_r} = \frac{{|x - a|}}{x} $

(6)

式中，E_r为相对误差；x为测量值，即优化后目标指数的均值；a为真实值，即优化前目标变量的均值。

所有模拟过程、指数计算和图形绘制均在R v4.1.3统计软件中实现(Barcaroli, 2014)。采样站位图采用ArcGIS 10.8绘制。

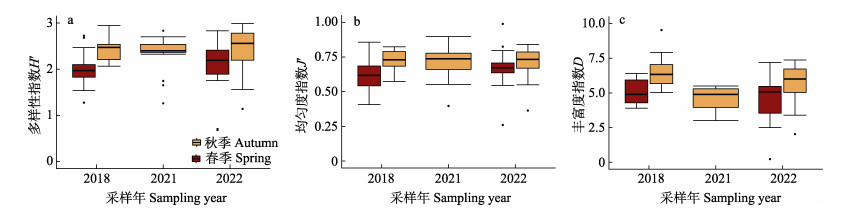
2 结果 2.1 茂名海域游泳生物多样性

近5次茂名海域底拖网调查中，生物多样性指数在不同季节之间存在差异。具体而言，秋季的多样性指数(H′)和均匀度指数(J′)均高于春季调查，仅2021年秋季丰富度指数(D)低于2018年春季，其余年份丰富度指数(D)均为秋季高于春季(图 2)。5次调查中，多样性指数(H′)的均值范围为2.00~2.53，丰富度指数(D)的均值范围为4.43~6.54，均匀度指数(J′)的均值范围为0.62~0.70。多样性指数(H′)、丰富度指数(D)和均匀度指数(J′)均值分别为2.32、5.32和0.69 (表 1)。

2.2 分层抽样 2.2.1 春季

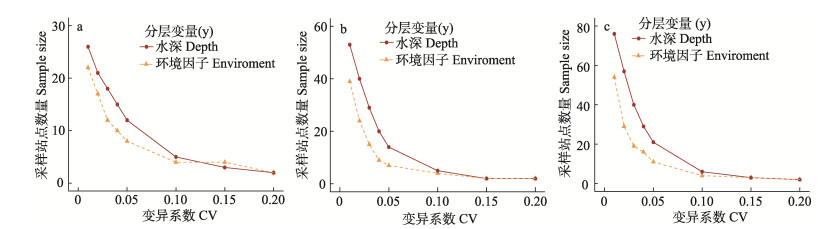
随着最大变异系数(CV)减小，春季的采样站点数量呈逐渐增加的趋势(图 3a、表 2和表 3)。当CV > 0.1时，CV值的减小对采样站点数量的影响相对较小，每减少0.05，采样站点数量增加1~2个或维持不变；然而，当CV < 0.1时，随着CV值的继续减小，采样站点数量变化幅度逐渐增加；当CV < 0.05时，采样站点数量变化幅度进一步增加；CV值从0.1减小至0.05，采样站点数量增加1倍；而当CV < 0.05时，CV值每减少0.01就需增加2~5个站点。

此外，CV值设置在0.2~0.01范围内，分层变量为环境因子和水深时，采样站点数量的变化范围分别为2~22和2~26。在相同CV值的限制下，以水深为分层变量时，所需的采样站点数量略高于以环境因子为分层变量，但在CV=0.15时，所需的采样站点数量比以环境因子为分层变量时少1个站点。

2.2.2 秋季

秋季的情况与春季相似，采样站点数量随CV的减小而增加(图 3b、表 2和表 3)。当CV > 0.1时，减小CV值对采样站点数量的影响相对较小，每减少0.05增加0~3个采样站点；当CV < 0.1时，减小CV值所需采样站点数量变化幅度增加；当CV值继续减小至 < 0.05时，所需采样站点数量变化幅度进一步增加；CV值每减少0.01所需站位增加2~15个。此外，以环境因子和水深为分层变量进行优化时，所得的采样站点数量范围分别为2~39和2~53。在相同CV值的限制下，以水深为分层变量时，所需采样站点数量通常高于以环境因子为分层变量时的采样站点数量。

与春季相比，CV=0.05时，各季节优化所得站点无明显差异；然而，当CV继续减少时，随着CV值的持续减小，春秋两季的优化采样站点数量差异逐渐增加。当CV=0.01时，以环境因子为分层变量的春季和秋季优化所得站位分别为22和39，而以水深为分层变量时所需站位分别为26和53。

2.2.3 不区分季节

在不考虑时间影响的情况下，与春秋季节相似，随着最大变异系数减小，所需采样站点数量增加(图 3c、表 2和表 3)。CV值在0.2~0.1范围内变化时，采样站点数量变化幅度相对较小，CV值每减小0.05，站点数量增加1~3个；CV值从0.1减小至0.05时，采样站点数量变化增大，以环境因子分层和水深分层时采样站点数量分别增加7和15；CV值继续减小至 < 0.05时，采样站点数量大幅度增加，每减小0.01采样站点数量增加3~25个。

在相同CV下，忽略时间影响时所需的采样站点数量大部分高于春、秋季。当CV=0.05时，以环境因子和水深为分层变量时，采样站点数量分别为11和21个，均高于春秋两季；当CV=0.01时，以环境因子和水深为分层变量时，采样站点数量分别为54和76个，远高于其他CV值下的站位数。

随着数据量的增加，相同CV值的所需采样站点数量增加。秋季数据包含61站点，约为春季站点数的2倍。在相同CV值下，秋季优化得到的站点数普遍高于春季。而在不考虑时间影响的数据中包含90个站点，在相同CV值下，优化得到的采样站点数量远高于考虑季节影响的结果。区分季节优化CV=0.05时，优化得到的采样站点数量为8、7和12、14，而不区分季节所需的采样站点数量达到了11和21个。

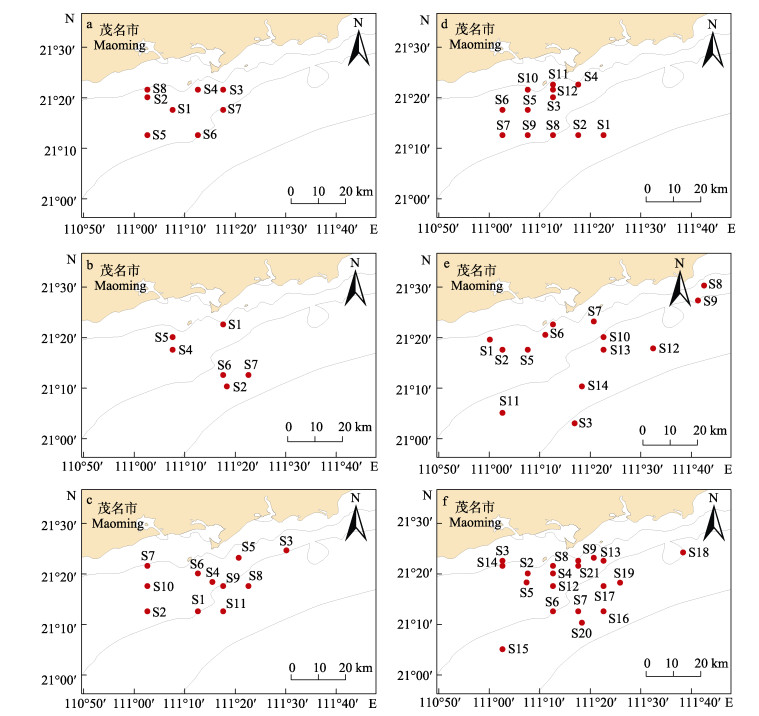
2.3 采样方案

采样站点数量随着CV值减小而增加，但当CV从0.05继续减少时，采样站点数量随着CV变化的幅度增加，CV值每减少0.01就需要增加1个站点或更多站点。在渔业资源调查中，增加1个站位所需的成本高、代价大。在CV=0.05时，可以保证数据的精确度，同时降低采样成本。在CV=0.05时，以环境因子分层，春季需8个采样站点，秋季和不区分季节分别需7和11个采样站点；而在以水深为分层变量时，春季需12个采样站点，秋季和不区分季节分别需14和21个采样站点(图 4)。通过“selectSample”函数选择优化后满足CV=0.05要求的样本，采样设计及各层权重详见附表 1和附表 2。

根据相对误差分析，建议采用以水深作为分层变量的方法，此时各指数相对误差均值较小。以环境因子和水深为分层变量时，各指数相对误差均值分别为2.38、2.02、2.85和0.43、3.14、1.74。以水深为分层变量时，除均匀度指数外，其他指数的相对误差均值较小，相对于以环境因子为分层变量时的相对误差均值较低(表 4和表 5)。

3 讨论

本研究基于茂名海域底拖网渔业资源调查数据，聚焦于生物多样性优化采样站点设计。研究结果显示，生物多样性指数存在季节差异，秋季生物多样性指数高于春季。此外，采样站点数量随着最大变异系数的减小而增加，且各季节之间变化趋势类似。

随着CV值减少，采样站点数量增加，在CV值减少至0.05时，站点数量增加幅度变大。这与抽样学理论相符，即随着样本量增加，数据精确度提高，样本量增加至一定量时，对精确度影响不大(冯士雍等, 1998; Lohr, 2009; 王晶等, 2017)。说明在茂名海域进行以生物多样性为目标的调查时，通过分层采样可以减少调查站位，同时，设置CV=0.05可以进一步优化站位数，降低渔业资源调查的成本，同时满足一定的精确度要求。

分层抽样是一种用于提高抽样估计准确性的方法，它将数据划分成不同层次，并在这些层次之间进行随机抽样。当层次间的异质性高于物种分布的层内异质性时可以提高抽样估计的精确度(Xu et al, 2015)。在渔业资源调查中通常使用与渔业生物分布密切相关的因子作为分层标准，如水深、底质、河口和地理区域等(赵静等, 2014; Xu et al, 2015; 韩青鹏等, 2019)。在SamplingStrata数据包中，分层变量的选择是基于它们与目标变量的相关性进行的。选择与目标变量高度相关的分层变量有助于更好地进行分层抽样，从而提高结果的准确性。本研究表明，在茂名海域调查时，将水深作为唯一的分层变量相对于多个环境因子更为适宜，更有助于提高抽样结果的准确性。以往的研究主要集中在优化站位分层或固定分层优化样本的分配，且在以西格兰虾(Pandalus borealis)、大西洋鳕(Gadus morhua)以及鲈鱼(Sebastes alutus)为研究对象的研究中指出，优化样本的分配更能提高估计的精确度(Gavaris et al, 1987; Carlsson et al, 2000; Folmer et al, 2000; Lunsford et al, 2001)。然而，本研究综合考虑了分层和样本分配优化，结果发现，在满足CV=0.05的要求下，茂名海域的渔业资源调查采样站点数量可以进一步减少。

SamplingStrata数据包提供了一种适用于多分层变量以及多目标变量的情景下实现最佳分层抽样的方法，最佳的分层策略在很大程度上受特定样本调查需求的制约，因此，应根据具体的调查目标选择分层方法。分层变量、目标变量以及精度要求是获得最佳分层策略的主要因素(Barcaroli, 2014)。其中，精度要求是以每个目标变量的最大变异系数表示(Barcaroli, 2014; Oyafuso et al, 2021)。该方法可以为不同的目标变量设置相同的精度要求。与传统的分层抽样方法相比，该方法可确保优化结果中各目标变量的精度都处于相近水平，不会出现明显的偏差，因此，可以保证优化后的分层样本中3个多样性指数的精度水平不存在大幅度偏差。本研究以茂名海域为例，运用SamplingStrata数据包中的分层抽样方法优化采样设计，旨在维持一定精确度的前提下减少采样站点数量，为后期渔业资源调查站位设计提供参考。

通常渔业资源调查目标有群落组成、体长分布和资源量指数等多种调查目标(王家启等, 2017; 孟新翔等, 2020; 张国晟等, 2021a)，对于多目标渔业资源调查，需综合考虑各调查目标的要求来设计采样站点。本研究仅以生物多样性为调查目标，后期可综合多个渔业资源调查常用的调查目标，进行多个目标的优化，以便更好地适应茂名海域渔业资源调查的需求。

附表