2. 大连理工大学 海岸与近海工程国家重点实验室 大连 116024
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024
人工鱼礁是一种人工构造物,将其投放到海底后,周围的水体压力受到海流与波浪的影响发生变化并产生新的流态。投放人工鱼礁通过背涡流的扰动与上升流的涌升,可以改善海区水质状况,增加渔业资源量,是一种可持续发展的新型生产模式(张艳等, 2013; 许强等, 2018)。鱼礁表层的附着生物是礁体集鱼的主要生物环境因子,也是礁区鱼类对象的主要饵料生物,鱼礁可以作为海洋鱼类的饵料场、栖息地及庇护所,具有较高的生态效益(李真真等, 2017; 李娇等, 2018; 张雪等, 2018)。人工鱼礁功能的实现和使用年限与其力学稳定性息息相关,需确保鱼礁在波浪和水流作用下,不会发生滑移、翻滚和沉陷而导致鱼礁被移动和掩埋(唐振朝等, 2011)。单纯水流时,礁体受力主要与雷诺数有关,超临界区时,礁体阻力系数大体稳定。波浪运动类似于往复震荡流动,区别之处为水质点沿椭圆轨迹运动,波动水流绕过礁体时,需同时关注沿椭圆轨迹2个轴向的影响。波浪对人工鱼礁有较大的作用力,可直接影响鱼礁的安全性、耐久性及经济效益。因此,鱼礁结构的设计与投放须考虑特定波浪和水深条件下礁体的受力特性。
国内外学者关于人工鱼礁在波浪作用下的受力特性做了一些研究,包括理论分析、建立数值模型并辅助于物理模型实验方法。Düzbastılar等(2009)将波浪理论与人工鱼礁受力公式相结合,对不同波浪、水深、海床坡度及不同迎流方式下,几种人工鱼礁的安全性进行了研究分析,确定了鱼礁的安全重量和投放水深范围。吴子岳等(2003)根据波流动力学理论,计算了十字型人工鱼礁在波、流共同作用下的最大作用力。郑延璇等(2014)根据山东海区的波流状况,测量并计算了等边三角型人工鱼礁分别在波浪和水流作用下的最大作用力、抗漂移和抗翻滚安全系数。赵云鹏等(2015)采用物理模型实验和数值模拟方法,揭示了三角型镂空人工鱼礁的水动力系数与Kc数和Re数的关系。
目前,关于人工鱼礁波浪受力特性的数值模拟计算研究相对较少,尤其是波浪的非线性对鱼礁受力的影响研究更加缺乏。为此,以一种镂空圆台型人工鱼礁为研究对象,先通过非线性分析方法对计算鱼礁受力常采用的Morison方程进行理论分析,提取无量纲数的主要非线性影响因子;再采用计算流体力学方法对礁体在非线性二阶Stokes波浪作用下的受力进行计算,得出更加接近实际波浪情况的鱼礁受力特性;最后,根据水平波浪力数值计算结果对礁体的稳定性进行校核,为鱼礁安全稳定性评估提供一种可靠的计算手段。
1 材料与方法 1.1 Morison方程与非线性波浪力理论分析一般而言,人工鱼礁属于小尺度构造物,工程上可采用Morison方程对其波浪荷载进行理论评估计算。由线性波浪理论确定的波浪场与实际波浪流速分布有较大差别,对求解鱼礁波浪力会产生一定局限性,需进一步采用精确的非线性波浪理论分析礁体波浪力。参照水平圆柱上非线性波浪力分析方法(薛鸿超等,1983),依托二阶Stokes波浪理论,对鱼礁波浪力的水平分力进行非线性分析。
按照Morison公式,鱼礁在波浪作用下,其单位高度上波压力的水平分力(Fx)公式如下:
| $ {{F}_{x}}={{F}_{dx}}+{{F}_{mx}}=\frac{1}{2}{{C}_{dx}}B\rho u|u|+{{C}_{mx}}B\times W\rho \frac{du}{dt} $ | (1) |
式中,Fdx和Fmx分别为速度力和惯性力在水平方向上的分量;Cdx和Cmx分别为速度力系数和惯性力系数;u为波浪质点水平速度;du/dt为波浪质点水平加速度;B和W分别为礁体的有效宽度和厚度;ρ为海水密度。
式(1)可以写成如下无量纲形式:
| $ \frac{{{F}_{x}}}{\gamma {{H}^{2}}}=\frac{{{F}_{dx}}}{\gamma {{H}^{2}}}+\frac{{{F}_{mx}}}{\gamma {{H}^{2}}}={{k}_{dx}}{{C}_{dx}}\frac{u}{C}\left| \frac{u}{C} \right|+{{k}_{mx}}{{C}_{mx}}\left(\frac{du}{dt}\times \frac{T}{C} \right) $ | (2) |
式中,H为波高;T为周期;C为波速;系数kdx=BC*/2H,kmx=BWδC*/H2,C*=C2/gH为特征波速;波陡δ=H/L,L为波长,均为已知值;水的比重γ与重力加速度g都是常值。
式(2)表明,鱼礁水平分力Fx计算的正确与否主要同波浪场的u/C和(du/dt)×(T/C)值,以及Cdx和Cmx值有关。波浪场坐标x轴为静水面,正向与波向线一致;z轴与静水面垂直,向上为正。根据二阶Stokes波浪理论(邹志利, 2005),其势函数ϕ比线性理论增加一个二阶项,即
| $ \begin{align} & \phi =\frac{H}{2}C\frac{\text{cos}\ hk(z+h)}{\sin \ hkh}\sin \theta + \\ & \ \ \ \ \frac{3}{8}{{\left(\frac{H}{2} \right)}^{2}}kc\frac{\cos \ h2k(z+h)}{\sin \ {{h}^{4}}kh}\sin 2\theta \\ \end{align} $ | (3) |
式中,波速C的表达式与线性波浪理论下相同,θ为相位角;k为波数;h为水深,z为高程;按定义u=-∂ϕ/∂x,由式(3)可得:
| $ \frac{u}{C}={{K}_{1}}\ \text{cos}\theta +{{K}_{2}}\ \text{cos}2\theta $ | (4) |
| $ \frac{{du}}{{dt}}\frac{T}{C} = - 2{\rm{ \mathsf{ π} }}{K_1}{\rm{sin}}\theta - 4{\rm{ \mathsf{ π} }}{K_2}{\rm{sin}}2\theta $ | (5) |
| $ {K_1} = {\rm{ \mathsf{ π} }}\delta \frac{{\cos \;hk(z + h)}}{{\sin \;hkh}}, {K_2} = \frac{3}{4}{{\rm{ \mathsf{ π} }}^2}{\delta ^2}\frac{{\cos \;h2k(z + h)}}{{\sin \;{h^4}kh}} $ | (6) |
式中,K1和K2中均包括πδ和kh 2个非线性因子,其中,kh=2πηδ,η=h/H为相对水深,故主要非线性因子实质为波陡δ。与线性波浪理论相比,随着δ的增大,Morison受力计算公式中的u/C和(du/dt) × (T/C)值变幅更加显著,非线性作用加强。
1.2 研究方法线性波浪理论忽略了波陡平方项,如果波陡较大,线性近似求解受力就更加不合理。因此,非线性波浪作用下,鱼礁受力数值模拟计算对获得更真实、更准确的鱼礁波浪力具有重要意义。鉴于此,借助FLUENT软件,通过二次开发编制造波程序,实现二阶Stokes波浪的数值模拟,进而获得鱼礁周围的波浪场和压力场分布,并进一步分析波陡变化对鱼礁水平波浪力大小及其稳定性的影响。
1.2.1 数学控制方程计算流体力学数值模型中,对不可压缩黏性流体的自由表面流动问题,整个流场采用连续性方程以及以速度和压力为变量的不可压缩黏性流体的N-S方程(邹志利, 2005)。
(1) 连续性方程公式:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 $ | (7) |
(2) 动量方程公式:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} = \\ \;\;\;\;\;\;\; - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {f_x} + v\left({\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right) + {S_x} \end{array} $ | (8) |
| $ \begin{array}{l} \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} = \\ \;\;\;\;\;\;\; - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {f_y} + v\left({\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right) + {S_y} \end{array} $ | (9) |
| $ \begin{array}{l} \frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}} = \\ \;\;\;\;\;\;\; - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + {f_z} + v\left({\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) + {S_z} \end{array} $ | (10) |
式中,u、v、w分别为x、y、z方向速度分量;t为时间;ρ为流体密度值;p为压强;fx、fy、fz为x、y、z方向的单位重力分量;υ为流体的运动黏度系数;Sx、Sy、Sz为x、y、z方向的附加动量源项。
1.2.2 二阶Stokes波浪理论依据二阶Stokes波浪理论,有限振幅波的波面方程和水质点运动速度方程如下(刘霞等, 2010):
波面方程公式:
| $ \begin{array}{l} \eta (x, t) = \frac{H}{2}{\rm{cos}}(\theta) + \\ \;\;\;\;\;\frac{H}{8}\left({\frac{{{\rm{ \mathsf{ π} }}H}}{L}} \right)\frac{{{\rm{cos}}\;hkh}}{{{\rm{sin}}\;{h^3}kh}}(cos\;h2kh + 2)cos\;2\theta \end{array} $ | (11) |
质点水平速度公式:
| $ \begin{array}{l} u = \frac{{{\rm{ \mathsf{ π} }}H}}{T}\frac{{\cos \;hk(z + h)}}{{\sin \;hkh}}\cos \;\theta + \\ \;\;\;\;\;\frac{3}{4}\frac{{{\rm{ \mathsf{ π} }}H}}{T}\left({\frac{{{\rm{ \mathsf{ π} }}H}}{L}} \right)\frac{{{\rm{cos}}\;h2k(z + h)}}{{\sin \;{h^4}kh}}\cos \;2\theta \end{array} $ | (12) |
质点垂直速度公式:
| $ \begin{array}{l} v = \frac{{{\rm{ \mathsf{ π} }}H}}{T}\frac{{\sin \;hk(z + h)}}{{\sin \;hkh}}\sin \theta + \\ \;\;\;\;\;\;\;\frac{3}{4}\frac{{{\rm{ \mathsf{ π} }}H}}{T}\left({\frac{{{\rm{ \mathsf{ π} }}H}}{L}} \right)\frac{{\sin \;h2k(z + h)}}{{\sin \;{h^4}kh}}\sin 2\theta \end{array} $ | (13) |
式中,T、k、H、h分别为波浪周期、波数、波高和静水深。
1.2.3 三维波浪数值水槽模型在Stokes波浪理论中,特征参数h/L(静水深与波长比值)的适用范围为0.05~0.50 (刘霞等, 2010);南海一般浅海波的波陡为1/15~1/20 (刘同渝等, 1987)。为便于物理模型实验验证,根据重力相似准则选定数值模型比例尺为1:10,模型静水深固定值为0.8 m,波浪周期均取1.8 s,对应波长约为4.21 m,波高及对应波陡值参数见表 1。
|
|
表 1 数值模拟波浪参数 Tab.1 Wave parameters for numerical simulation |
从图 1可以看出,波浪数值水槽模型计算尺寸为20.0 m(长)×2.0 m(宽)×1.8 m(深),静水深为0.8 m,坐标系原点位于造波边界的静水面处。基于二阶Stokes波浪理论,采用边界造波法,即根据行波的波形和速度解析公式(11)~公式(13),在左侧造波边界给定水体的流速(Ux和Uy)和波高(H)进行三维波浪模拟。模型顶部为压强边界;底部为固壁无滑移边界;右侧为压力出流边界,该边界处沿水面向下给定静水压强,可以使水体随计算区域内的压强变化自由流出、流进,保证该区域内水深为一个定值。依据物理模型实验阻尼消波原理,在水槽末端布置1~2倍波长海绵层阻尼消波,在动量方程中添加阻尼项达到消除该区域的波动(董志等, 2009; 韩朋等, 2009)。
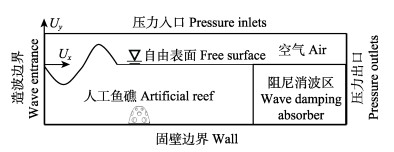
|
图 1 波浪数值水槽模型 Fig.1 Numerical wave flume model |
波浪数值水槽中存在空气和水两相流动,适宜采用VOF(Volume of fluid)方法追踪自由水面。基于有限体积法,采用中心差分格式对控制方程扩散项进行离散;对流项中压力方程运用Body Force Weighed格式,压力速度耦合方式使用PISO算法开展迭代计算;动量方程离散项采用二阶迎风格式进行计算;时间差分采用全隐式格式。
1.2.4 人工鱼礁模型及网格划分一种镂空圆台型人工鱼礁,是在传统圆台人工鱼礁结构基础上改进而成。礁体上方圆台部分四周及顶部设有圆孔,内部及底面均为镂空结构,能够诱集鱼群以及为鱼类栖息和繁育提供庇护所;中间十字竖板可增强圆台内上升流强度,提高水循环效率;正方形底座可加强礁体稳定性。鱼礁模型根据重力相似准则,按照1:10模型比例设计,具体构架尺寸及整体构造见图 2。
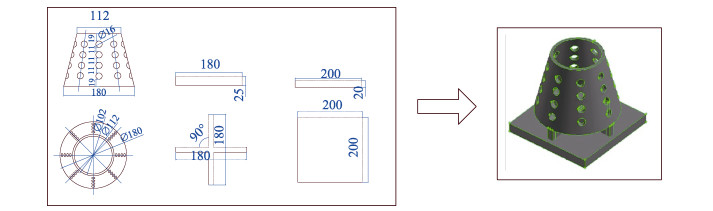
|
图 2 鱼礁模型结构与尺寸(mm) Fig.2 The construction and size of artificial reef model (mm) |
圆台型鱼礁构造复杂,须分区划分网格,礁体周围区域采用四面体非结构网格,可更好适应礁体结构,水槽其他区域均为六面体结构网格。为准确捕捉波面运动轨迹,提高波传播时的计算精度,在自由水面附近采用渐变网格,即对水体表层附近网格进行加密。在进行礁体受力数值模拟计算之前,对网格的适应性进行验证,最终确定计算网格见图 3。
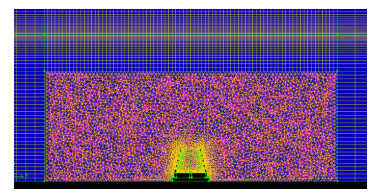
|
图 3 鱼礁网格划分 Fig.3 Mesh division of artificial reef |
以人工鱼礁(x=5.0 m)正上方波形为代表,对数值模拟的波浪波幅进行时程监控。波浪传播稳定后,不同波陡值二阶Stokes波浪单个周期内波幅的数值解与解析解对比见图 4。从图 4可以看出,礁体上方波浪波幅的数值解和解析解吻合较好,保证数值计算结果的正确性与可靠性。

|
图 4 二阶Stokes波幅历时时程数值解与解析解 Fig.4 Comparisons of analytic solutions and numerical results of the second order Stokes wave amplitudes |
图 5是三维波浪数值水槽末端消波区域“x=18 m”位置处的波面时间过程线。从图 5可以看出,该区域内波幅几乎为零,自由水面始终位于零点附近,表明由造波区传播过来的波能很好地被数值“消波器”吸收,海绵层用于消除非线性规则波也相当有效。
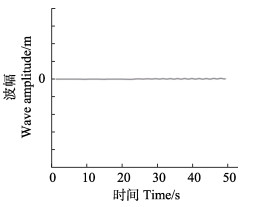
|
图 5 消波区“x=18 m”处波面历时过程线 Fig.5 The numerical results of wave profile at "x=18 m" |
以波陡1/17.5 (波高H4=0.24 m)波浪工况为例,分析鱼礁正向和负向最大水平受力时的波浪场与压力场。从图 6可以看出,鱼礁在承受正向最大水平波浪力时,穿过礁体的整体波浪流场线为正向,波峰位于礁体水平前方约1/6波长处;负向最大水平受力时,整体波浪流场线为负向,礁体在波谷后方约1/6波长位置;2种受力条件下,鱼礁周围流场均发生显著变化。与线性波相比,二阶Stokes波浪理论波面会升高,波峰变尖,波谷变平坦(图 6)。从图 7可以看出,鱼礁波浪压力场中,正向最大水平受力时,礁体前方压强较后部压强大,并取得最大正压差值;负向最大水平受力时与之相反。波浪运动对鱼礁周围流场及压力场分布影响作用明显,从而对其受力大小改变显著。

|
图 6 鱼礁周围波浪场流线(z=0; δ=1/17.5) Fig.6 The wave field streamline chart around artificial reef (z=0; δ=1/17.5) |

|
图 7 鱼礁周围波浪场压强(z=0; δ=1/17.5) Fig.7 The wave field pressure chart around artificial reef (z=0; δ=1/17.5) |
从图 8可以看出,不同波陡波浪作用时,1个周期内鱼礁的水平波浪力大小,每间隔0.1 s提取1次受力值,表面波幅历时变化与图 4保持一致。结合图 4与图 8可以看出,鱼礁受力随着波浪运动呈正、负变化,当鱼礁正上方波面从下方恢复到自由水面时,产生正向最大水平受力;在波面从最大值回落到自由水面附近时,取得负向最大水平受力。波浪处于上跨零点和下跨零点时,水平速度为零,加速度最大,礁体的速度力为零,惯性力为最大值,这与赵云鹏等(2015)对人工鱼礁最大波浪力产生较大影响的是惯性力的结论较为吻合。同一波面,随着波陡值的增加,鱼礁受力逐渐增大,在受力绝对值较大时,这一规律最为明显。

|
图 8 单周期内不同波陡波浪作用下鱼礁水平波浪力 Fig.8 The horizontal wave force on the artificial reef with different wave steepness in one period |
鉴于各工况受力结果,通过回归分析方法得出,波陡值与礁体正、负向最大水平受力分别呈正、负线性增长关系,并将其绘制于图 9中。由线性回归分析方法所得正向最大水平受力(Fmax)与波陡(δ)的最佳关系方程:Fmax=–0.89+110.44δ,相关系数(R2)为0.9795;负向最大水平受力(F–max)与波陡(δ)的最佳关系方程:F–max=–0.10–83.52δ,相关系数(R2)为0.9899。上述2组关系式可作为镂空圆台型式人工鱼礁,在二阶Stokes波浪作用下水平波浪力的估算公式。
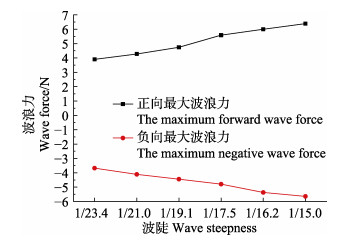
|
图 9 不同波陡波浪作用下鱼礁正向与负向最大水平波浪力 Fig.9 The maximum horizontal wave force on the artificial reef with different wave steepness |
鱼礁的物理稳定性与礁区底质、投放技术及本身结构有关,对礁体功能的正常实现至关重要。依据圆台型鱼礁水平波浪力数值计算结果,对其在波浪作用下的漂移与翻滚安全性分别进行计算验证。参考相关文献选取以下参数值(吴子岳等, 2003; 郑延璇等, 2014),人工鱼礁多为钢筋混凝土材质,礁体密度σ取3100 kg/m3,水平均匀摩擦系数μ为0.5,海水密度ρ为1025 kg/m3。假设礁区底部均匀平整,礁体水平摆放。
2.4.1 漂移安全性校核漂移安全性指鱼礁在最大水平波浪力作用时不发生滑动,即要求其底摩擦力大于最大水平波浪力。不漂移安全系数为S;静摩擦力公式:
| $ {F_M} = \mu V(\sigma - \rho) $ |
式中,V为礁体实体体积。
最大波浪力绝对值Fwmax,则需满足S=FM/Fwmax > 1。
图 10为鱼礁在不同波陡波浪作用下的不漂移安全系数,漂移临界值指不漂移系数刚好为1的情况,此时,礁体处于发生漂移的临界状态。从图 10可以看出,随着波陡的增加,不漂移安全系数S逐渐减小,在最小与最大波陡工况下分别为3.45与2.11,礁体不会发生漂移。
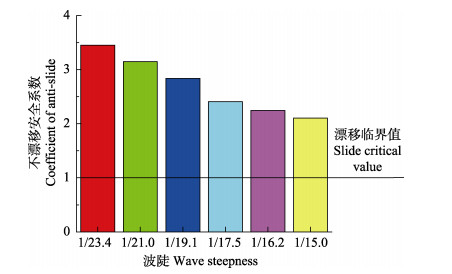
|
图 10 不同波陡时鱼礁在水平均匀底质上的不漂移安全系数 Fig.10 The calculated coefficient of anti-slide of artificial reef on horizontal plane under different wave steepness |
翻滚安全性指鱼礁在最大水平波浪力作用下不发生翻滚,要求礁体的重力与浮力合力矩Mar大于最大水平波浪力矩Mwmax,即满足不翻滚安全系数M=Mar/Mwmax > 1。鱼礁沿x、z轴对称分布,其重心位于y轴上,因此,礁体重力与浮力合力矩公式为:
| $ {M_{{\rm{ar}}}} = L \times V(\sigma - \rho)/2 $ |
式中,L为底边长。
鱼礁空间结构设计复杂,需简化计算水平波浪力力矩。假设最大水平波浪力荷载均匀分布于鱼礁表面,可得其受力分布密度:d=Fwmax/S。
式中,S为礁体表面积。则Mwmax值可由鱼礁表面每个单元面上的受力分布密度d与力臂y的乘积结果对鱼礁表面进行积分求和获得。6种波陡下,鱼礁的不翻滚安全系数见图 11。从图 11可以看出,其最大值为7.54,最小值为3.96,均处于翻滚临界值以上区域,礁体不会发生翻滚。
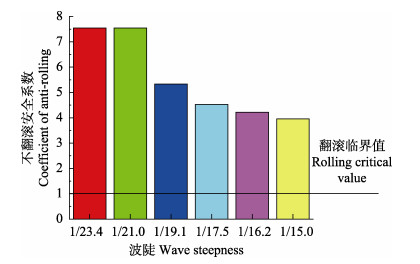
|
图 11 不同波陡时鱼礁在水平均匀底质上的不翻滚安全系数 Fig.11 The calculated coefficient of anti-rolling of artificial reef on horizontal plane under different wave steepness |
圆台型人工鱼礁主体为镂空结构,内部空间充裕、重心较低、附着面积充足,整体结构沿水深方向对称分布,投放到海底后,可充分适应不同方向的水流与波浪情况。首先,基于非线性分析方法,运用Stokes二阶波浪理论,对适用于人工鱼礁水平波浪力计算的Morison方程进行无量纲分析,提出鱼礁波浪受力的主要非线性影响因子为波陡项,并随着波陡的增大,非线性作用逐渐加强。其次,在理论分析基础上,采用计算流体力学方法,建立了求解鱼礁波浪力的三维非线性波浪数值水槽模型。
数值结果分析部分给出了二阶Stokes波波幅历时数值解与解析解对比结果,以及消波区内自由水面的运动分布结果,表明波浪模拟准确。鱼礁受力计算正确与否,与波浪场分布情况密切相关,实践中更多关注礁体最大受力时的波浪运动状态。因此,本研究中分别给出鱼礁在取得正、负向最大受力时,中轴面上的波浪场结构与压力场分布。数值模型中,鱼礁水平波浪力值是通过将礁体全部边界网格面上的压力、粘性力与水平方向矢量做点积,然后,再将所有边界网格上的点积求和得出。同一波陡波浪作用下,鱼礁水平波浪力作周期性正、负大小变化;正、负向最大水平波浪力随着入射波波陡的增加分别呈正、负线性增长。常见的十字型、钢制四方台、回字型与等边三角型人工鱼礁在相似波况下的平均不漂移系数分别为1.58、1.44、1.78、1.51;平均不翻滚系数为1.63、2.23、2.36、3.16 (吴子岳等, 2003; 钟术求等, 2006; 许柳雄等, 2010; 郑延璇等, 2014)。本圆台型鱼礁的不漂移系数与不翻滚系数分别为2.1和4.0,高于其他型状鱼礁,在稳定性方面有较大的提高。
4 结论本研究结果显示,圆台型人工鱼礁整体不漂移与不翻滚性能优越,在大波陡波浪作用下,能够保持良好的稳定性,并具有良好的流场效应,是一种高性能的人工鱼礁。本研究在非线性波浪理论分析基础上,提出了一种精确求解鱼礁水平波浪力的数值计算方法,相比物理模型实验方法,具有低成本、高效率的优点。本数值模拟与分析方法也可为其他形状人工鱼礁,在非线性波浪作用下的水平受力及其稳定性评估计算提供重要参考,并具有广泛的适用性。
Dong Z, Zhan ZM. Comparison of existing methods for wave generating and absorbing in VOF-based numerical tank. Chinese Journal of Hydrodynamics, 2009, 24(1): 15-21 [董志, 詹志民. 基于VOF方法的数值波浪水槽以及造波消波方法研究. 水动力学研究与进展: A辑, 2009, 24(1): 15-21] |
Düzbastılar FO, Şentürk U. Determining the weights of two types of artificial reefs required to resist wave action in different water depths and bottom slopes. Ocean Engineering, 2009, 36: 900-913 DOI:10.1016/j.oceaneng.2009.06.008 |
Han P, Ren B, Li XL, et al. Study on damping absorber for the irregular waves based on VOF method. Journal of Water Way and Harbor, 2009, 30(1): 9-13 [韩朋, 任冰, 李学临, 等. 基于VOF方法的不规则波数值波浪水槽的阻尼消波研究. 水道港口, 2009, 30(1): 9-13 DOI:10.3969/j.issn.1005-8443.2009.01.002] |
Li J, Zhang Y, Yuan W, et al. Research on artificial reef ecosystem health assessment based on fuzzy synthetic evaluation. Progress in Fishery Sciences, 2018, 39(5): 10-19 [李娇, 张艳, 袁伟, 等. 基于模糊综合评价法的人工鱼礁生态系统健康研究. 渔业科学进展, 2018, 39(5): 10-19] |
Liu TY, Chen QE, Huang RK, et al. Test on artificial fish reef model in wave flume. Marine Fisheries, 1987, 18(1): 9-12 [刘同渝, 陈勤儿, 黄汝堪, 等. 鱼礁模型波浪水槽试验. 海洋渔业, 1987, 18(1): 9-12] |
Liu X, Tan GH, Wang DG. Numerical simulation of second-order Stokes based on wave-generation method of defining inlet boundary conditions. Journal of Liaoning Technical University (Natural Science), 2010, 29(1): 107-111 [刘霞, 谭国焕, 王大国. 基于边界造波法的二阶Stokes波的数值生成. 辽宁工程技术大学学报(自然科学版), 2010, 29(1): 107-111 DOI:10.3969/j.issn.1008-0562.2010.01.028] |
Li ZZ, Gong PH, Guan CT, et al. Study on the organisms attachment of artificial reefs constructed with five different cements. Progress in Fishery Sciences, 2017, 38(5): 57-63 [李真真, 公丕海, 关长涛, 等. 不同水泥类型混凝土人工鱼礁的生物附着效果. 渔业科学进展, 2017, 38(5): 57-63] |
Tang ZC, Chen PM, Jia XP. Study on safe weight of artificial reef in different water depths and bottom slopes under Daya Bay wave. Journal of Fisheries of China, 2011, 35(11): 1650-1657 [唐振朝, 陈丕茂, 贾晓平. 大亚湾不同波浪、水深与坡度条件下车叶型人工鱼礁的安全重量. 水产学报, 2011, 35(11): 1650-1657] |
Wu ZY, Sun MC, Tang W. The calculation of the hydrodynamic force of the artificial cross-reefs. Marine Fisheries Research, 2003, 24(4): 32-35 [吴子岳, 孙满昌, 汤威. 十字型人工鱼礁礁体的水动力计算. 海洋水产研究, 2003, 24(4): 32-35] |
Xue HC, Guo D, Yan YX. Non-linear analysis of wave force on horizontal cylinder. Ocean Engineering, 1983(1): 36-49 [薛鸿超, 过达, 严以新. 水平圆柱上波压力的非线性分析. 海洋工程, 1983(1): 36-49] |
Xu LX, Liu J, Zhang S, et al. Research on the design and stability calculation of the artificial Hui style reef. Journal of Wuhan University of Technology, 2010, 32(12): 79-83 [许柳雄, 刘健, 张硕, 等. 回字型人工鱼礁礁体设计及其稳定性计算. 武汉理工大学学报, 2010, 32(12): 79-83 DOI:10.3963/j.issn.1671-4431.2010.12.019] |
Xu Q, Liu W, Gao F, et al. Development of marine ranching at tropical island area in South China Sea-advantages, status and prospects. Progress in Fishery Sciences, 2018, 39(5): 173-180 [许强, 刘维, 高菲, 等. 发展中国南海热带岛礁海洋牧场--机遇、现状与展望. 渔业科学进展, 2018, 39(5): 173-180] |
Zhang X, Xu XF, Dai YY, et al. Phytoplankton community characteristics and variation in artificial reefs of Tianjin offshore. Progress in Fishery Sciences, 2018, 39(6): 1-10 [张雪, 徐晓甫, 戴媛媛, 等. 天津近岸人工鱼礁海域浮游植物群落及其变化特征. 渔业科学进展, 2018, 39(6): 1-10] |
Zhang Y, Chen JF, Guo F, et al. Variation of seawater at the artificial reef area in Laizhou Bay. Progress in Fishery Sciences, 2013, 34(5): 1-7 [张艳, 陈聚法, 过锋, 等. 莱州人工鱼礁海域水质状况的变化特征. 渔业科学进展, 2013, 34(5): 1-7 DOI:10.3969/j.issn.1000-7075.2013.05.001] |
Zhao YP, Wang XP, Dong GH. Numerical simulation and experimental validation of hydrodynamic characteristics of submerged artificial reef in waves. Ocean Engineering, 2015, 33(6): 52-61 [赵云鹏, 王晓鹏, 董国海. 波浪作用下三角型人工鱼礁水动力特性数值模拟与实验验证. 海洋工程, 2015, 33(6): 52-61] |
Zheng YX, Liang ZL, Guan CT, et al. Structure design and stability of the equilateral triangle artificial reef. Progress in Fishery Sciences, 2014, 35(3): 117-125 [郑延璇, 梁振林, 关长涛, 等. 等边三角型人工鱼礁礁体结构设计及其稳定性. 渔业科学进展, 2014, 35(3): 117-125] |
Zhong SQ, Sun MC, Zhang SY, et al. Study on the design and stability of the artificial steel prism reef. Marine Fisheries, 2006, 28(3): 234-240 [钟术求, 孙满昌, 章守宇, 等. 钢制四方台型人工鱼礁礁体设计及稳定性研究. 海洋渔业, 2006, 28(3): 234-240 DOI:10.3969/j.issn.1004-2490.2006.03.011] |
Zou ZL. Water wave theories and their applications. Beijing: Science Press, 2005 [邹志利. 水波理论及其应用. 北京: 科学出版社, 2005]
|



