动态能量收支(Dynamic energy budget, DEB)理论是Kooijman(1986)基于κ原则提出的，描述生物摄食同化的能量一部分(κ)用于维持身体结构生长，另一部分(1–κ)用于性腺成熟和繁殖储备(Kooijman, 2000)。依据DEB理论而建立的个体生长模型，又称动态能量收支模型、DEB模型，不仅能够量化能量在整个生物生活史阶段的分配情况(Sousa et al, 2010; Ren et al, 2001；Kooijman, 2010)，而且能够模拟生物在一段时期内的生长状况。DEB理论的关键是基于物种之间代谢的相似性，且都遵循κ原则。DEB模型是参数化模型，原则上相同的基础模型结构可用于所有的生物物种，模型表现出的物种在生命史上的差异主要是由于DEB参数集合的差异(Sousa et al, 2006)。因此，参数对于DEB模型的构建十分重要，参数越准确，模型的拟合效果越好(Ren et al, 2008; 张继红等, 2016)。目前，DEB模型已成功应用于水产养殖，包括鱼类(Orestis et al, 2019)、贝类(Bourlès et al, 2009)、大型海藻(蔡碧莹等, 2019)和海参(Ren et al, 2016)等。

皱纹盘鲍(Haliotis discus hannai)是我国重要的养殖经济贝类，主要分布在辽东半岛和山东半岛(常亚青等, 1998)。皱纹盘鲍含有丰富的营养成分，深受人们喜爱(Koizumi et al, 2017; 李太武等, 1995)。随着市场需求量的增大以及水产养殖技术的成熟，皱纹盘鲍已经实现大规模人工养殖(杨义等, 2007; 张晓梅等, 2010)。通过建立皱纹盘鲍个体生长模型，并进一步建立其养殖容量模型，对于指导养殖管理和评估养殖容量具有重要意义(刘慧等, 2018)。国内外对双壳滤食性贝类DEB模型的研究已有较多报道。国外已建立贻贝(Mytilus edulis) (Saraiva et al, 2012)、长牡蛎(Crassostrea gigas) (Rico-Villa et al, 2010)、蛤类(Macoma balthica; Cerastoderma edule) (van Hare et al, 1993)等的DEB模型；国内有虾夷扇贝(Patinopecten yessoensis)(张继红等, 2017)的DEB模型。由于国外鲍养殖相较于其他海产贝类品种较少，国内对数理模型的研究起步较晚，因此，单壳舐食性贝类(如鲍)DEB模型的研究较少，主要以传统能量方程的研究为主(Fang et al, 2018)。本研究参照国内外贝类生物DEB模型的研究方法，通过生理实验确定皱纹盘鲍DEB模型的6个相关参数，包括单位体积维持耗能率(Volume-specific maintenance costs, $[{\dot p_M}]$)、单位体积结构物质所需的能量(Volume-specificcosts for structure, $[{E_G}]$)、单位体积最大储存能量(Maximum storage density, $[{E_m}]$)、储备能量含量(Energy content of reserve, ${\mu _E}$)、形状系数(Shape coefficient, δm)和Arrhenius温度(Arrhenius temperature, )，可为皱纹盘鲍个体生长模型的构建奠定参数基础。

选取壳长为(5.91±0.26) cm的皱纹盘鲍用于饥饿实验。选取不同规格[分为3组：a组壳长为(2.37± 0.18) cm，b组为(4.65±0.11) cm，c组为(6.21±0.51) cm]分别用于温度对耗氧的影响实验和生物学测量。样品均取自山东省荣成市寻山集团。皱纹盘鲍去掉表层附着物之后置于实验室水槽中24 h充气暂养，暂养水温为(18±1)℃，盐度为30，暂养3 d，成活率稳定后开始正式实验。

实验于2018年9月~10月初、10月底~12月在威海长青海洋科技股份有限公司国家海产贝类研究中心实验室进行。

取同一规格、壳长为(5.91± 0.26) cm皱纹盘鲍70个，进行饥饿实验。实验期间不投饵，水温为皱纹盘鲍正常呼吸代谢的温度，控制在18℃左右，每7 d换水3次，保持水槽中的海水清洁且不含杂藻。每隔5~10 d取5个皱纹盘鲍，碘量法(GB/T 7489-87)测定其呼吸耗氧率，并测定其总湿重(W)、软组织湿重(WW)、软组织干重(DW)和软组织有机物含量(%)，软组织干重与呼吸耗氧率基本保持恒定时结束实验(35 d)。其中，总湿重为皱纹盘鲍体表无水后的全重量；软组织湿重为剥离壳之后，剩余全部软组织的鲜重；软组织干重为测定完软组织湿重之后，在60℃下的烘干箱烘干72 h的重量；软组织有机物含量根据灰分法(GB 5009.4-2016《食品安全国家标准食品中灰分的测定》)估算，即将称过干重的软组织进行碳化至无烟，然后转移到马弗炉中，在450℃下灼烧4 h后称重，质量差即为软组织有机物的含量。皱纹盘鲍不随饥饿时间而变化的呼吸耗氧率为单位体积维持耗能率：

式中，${R_t}$为皱纹盘鲍饥饿后基本恒定的呼吸耗氧率[mg/(ind.∙h)]，${E_o}$为O₂的能值(1 ml O₂ = 20.3 J)(Ren et al, 2008)，$t$为时间转化系数(1 d = 24 h)，${\rho _o}$为O₂在15℃下的密度(1.226 mg/ml)，为皱纹盘鲍的体积(cm³)。

皱纹盘鲍软组织干重不随饥饿时间变化时有机物的重量即为皱纹盘鲍单位体积结构物质所需的能量$[{E_G}]$：

式中，$k$为有机物的能值(23000 J/g) (Brey et al, 1988; van der Veer et al, 2006)，${W_t}$为实验结束时保持恒定的软组织干重(g)，${C_t}$为实验结束时贝类软组织有机物含量(%)，${T_r}$为生长效率的转换系数(${T_r}$ = 40%) (van der Veer et al, 2006)，为鲍的体积(cm³)。

鲍最大储存能量$[{E_m}]$为初始能量与饥饿后剩余的结构物质能量之差：

式中，为有机物的能值(23000 J/g)，为软组织干重的初始值(g)，${C_0}$为实验初始时皱纹盘鲍软组织有机物含量(%)，${W_t}$为实验结束时保持恒定软组织干重(g)，${C_t}$为实验结束时贝类软组织有机物含量(%)，为鲍的体积(cm³)。

储备能量含量${\mu _E}$为初始和终末能量之差与软组织干重之差的比值：

式中，为有机物的能值(23000 J/g)，为软组织干重的初始值(g)，${C_0}$为实验初始时鲍软组织有机物含量(%)，${W_t}$为实验结束时保持恒定的软组织干重(g)，${C_t}$为实验结束时贝类软组织有机物含量(%)。

将暂养的3种规格的皱纹盘鲍分为5组，每组5只，由室温18℃逐步升温或降温至5℃、10℃、15℃、20℃和25℃ 5个温度梯度，防止皱纹盘鲍因温度骤变不适应而死亡。溶解氧采用碘量法测定，耗氧实验进行1~2 h，在密闭的呼吸室中测定初始和终末耗氧率(DO)，并测定鲍的软组织干重(DW)。

单位干重耗氧率${\rm{OR}}$计算公式：

式中，${\rm{OR}}$为皱纹盘鲍单位干重耗氧率[mg/(g∙h)]，${\rm{D}}{{\rm{O}}_0}$为初始溶解氧(mg/L)，${\rm{D}}{{\rm{O}}_t}$结束时溶氧(mg/L)，${V_L}$为呼吸室体积(L)，为软组织干重(g)，${t_1}$为耗氧实验持续的时间(h)。

取100只不同规格的鲍测定其生物学参数，包括壳长(L)、总湿重(W)、软组织湿重(WW)及软组织干重(DW)。壳长用游标卡尺(精度0.01 mm)测量；重量采用电子天平(精度0.01 g)称量。体积(V)通常较难测量，一般根据软组织湿重和密度(1.1 g/cm³)的乘积得到(Sablani et al, 2004)。

式中，V为鲍的体积(cm³)；$\delta m$为形状系数；L为鲍的壳长(cm)；DW为鲍软组织干重(g)。

实验结果运用Excel 2016进行数据统计与线性回归估计并作图；采用SPSS 22.0分析软件进行单因素方差分析(One-way ANOVA)得到标准差，最终结果以平均值±标准差(Mean±SD)表示。

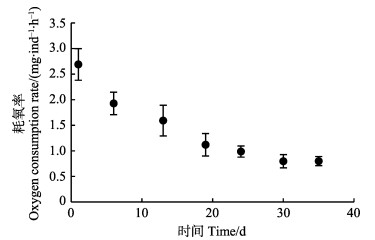
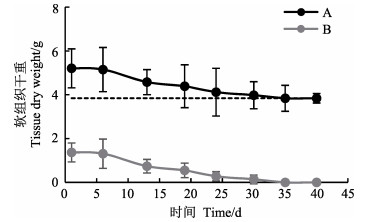
实验共进行35 d，期间不投喂。随着饥饿时间延长，皱纹盘鲍软组织干重和耗氧率逐渐降低。鲍呼吸耗氧率由最初2.69 mg/(ind.∙h)逐渐下降，到第30天左右逐渐稳定在0.8 mg/(ind.∙h) (图 1)，软组织干重由(5.21±0.89) g降低至(3.84±0.22) g(图 2)，并基本保持恒定。软组织干重和呼吸耗氧率较初始值下降26.3%和70%，皱纹盘鲍软组织有机物含量从80%降到58% (表 1)。

图 1(Fig. 1)

图 1 皱纹盘鲍耗氧率随饥饿时间的变化情况 Fig.1 The change of oxygen consumption rate of H. discus hannai with the starvation time

图 1(Fig. 1)

图 2 皱纹盘鲍软组织干重(A)和存储物质(B)随饥饿时间变化情况 Fig.2 Changes in dry flesh weight (A) and storage of reserves (B) in H. discus hannai during the starvation experiment

表 1(Tab.1)

表 1 饥饿实验相关参数计算值 Tab.1 Parameter calculation value related to the starvation experiment 项目Items 初始值Initial value 终末值End value 结果Result 软组织干重Dry flesh weight (g) 5.21±0.89 3.84±0.22 有机物含量Organic content (%) 80.00±6.01 58.00±4.65 单位体积结构物质所需的能量$[{E_G}]$ Volume-specific costs for structure, $[{E_G}]$(J/cm3) 8120±328 单位体积最大储存能量$[{E_m}]$ Maximum storage density, $[{E_m}]$(J/cm3) 2726±168 单位体积维持耗能率$[{\dot p_M}]$ Volume-specific maintenance costs, $[{\dot p_M}]$[J/(cm3∙d)] 20.18±2.71 储备能量含量μE Energy content of reserve, μE (J/g) 32583±2810

表 1 饥饿实验相关参数计算值 Tab.1 Parameter calculation value related to the starvation experiment

皱纹盘鲍在饥饿后耗氧率基本维持稳定，根据公式(1)计算得出单位体积维持耗能率$[{\dot p_M}]$的平均值为20.18 J/(cm³∙d)。

在饥饿实验25 d内，软组织干重下降明显，在35 d之后基本趋于稳定，根据公式(2)，将软组织干重转化为单位体积结构物质所需的能量值$[{E_G}]$，为8120 J/cm³。

根据公式(3)，将鲍饥饿实验初始时的能量值与饥饿后剩余能量的差值转化为单位体积最大存储能量$[{E_m}]$，为2726 J/cm³(表 1)；能量的差值与饥饿实验初始与结束时软组织干重差值的比值为储备能量${\mu _E}$，为32583 J/g。

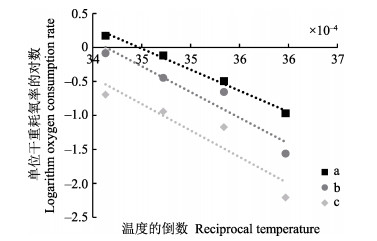
在实验条件下，3组皱纹盘鲍(表 1)单位干重耗氧率随个体大小的增加而减小(图 3)。耗氧率随温度呈先上升后下降的趋势，在5℃~20℃时，单位干重耗氧率随温度的升高而增大，在20℃达最高值；之后，随温度升高，单位干重耗氧率降低。在20℃转折点之前，依据温度对皱纹盘鲍单位干重耗氧率的关系，得出a、b、c组鲍耗氧率的ln值与温度(热力学温度)倒数的线性关系分别为lnR = –6201.1T^–1+21.377 (R² = 0.9914)、lnR = –7578.7T^–1+25.87(R² = 0.9126)、lnR = –7807.6T^–1+ 26.104(R² = 0.8656) (图 4)。3组方程斜率的绝对值的平均值为7196 K，即皱纹盘鲍的Arrhenius温度${T_A}$。

表 2(Tab.2)

表 2 3组皱纹盘鲍生物学特征 Tab.2 Biological characteristics of three groups of H. discus hannai 组别Group a b c 壳长Shell length (cm) 2.37±0.18 4.65±0.11 6.21±0.51 总湿重Shell-on wet weight (g) 1.28±0.27 10.90±2.58 28.75±5.60 软组织干重Dry flesh weight (g) 0.15±0.08 1.98±0.35 5.63±0.89

表 2 3组皱纹盘鲍生物学特征 Tab.2 Biological characteristics of three groups of H. discus hannai

图 1(Fig. 1)

图 3 不同大小的皱纹盘鲍在不同温度下的单位干重耗氧率 Fig.3 Oxygen consumption rate per unit dry weight of abalone at different sizes

图 1(Fig. 1)

图 4 皱纹盘鲍单位干重耗氧率的ln值与温度的倒数线性关系 Fig.4 Linear relationship between the logarithm value of the oxygen consumption rate per unit dry weight and the reciprocal temperature

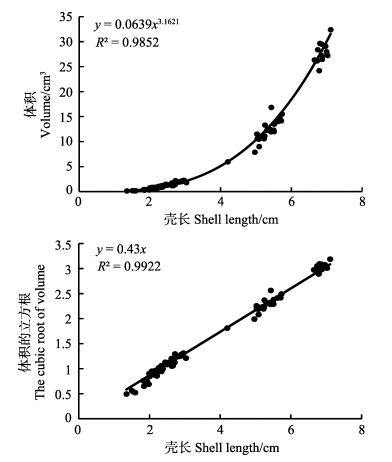
通过拟合回归，皱纹盘鲍壳长与体积符合三次函数(图 5)：V = 0.0639 L^3.1621(R² = 0.9852)，根据公式(6)壳长与软组织湿重的立方根线性回归的斜率(图 5)即为形状系数δm的值为0.43。

图 1(Fig. 1)

图 5 皱纹盘鲍壳长与软组织湿重的关系 Fig.5 The relationship between wet flesh weight and shell length for H. discus hannai

体积是模型输出状态变量的关键因素，形状系数δm是表征体积和表面积函数的重要参数，因此，δm值的获得对模型构建十分重要。因贝类的体积和表面积较难测量，通常使用间接法测定。一种方法是只有贝壳的情况下测定贝壳的重量，用密度为1 g/cm³物质(如马铃薯渣)填满贝壳再次称重(van der Veer et al, 2001、2006)，质量差为贝的物理体积，然后再通过公式$V = {(\delta m \times L)^3}$计算形状系数的值，这种方法测定的体积要比实际生物量要高(van der Veer et al, 2006)，δm的值也高。为使数据更准确，研究者通过另一种方法，直接测定软组织湿重，通过软组织密度转化获得。本研究根据后一种方法测定。

$[{E_G}]$和$[{\dot p_M}]$的值无法直接测量得出，根据van der Veer等(2006)总结的方法：$[{E_G}]$值可以通过计算贝饥饿后且死亡之前软组织干重乘以转换系数来计算；$[{\dot p_M}]$值通过测定随着饥饿时间的推移，呼吸耗氧率的变化来推算，但要注意饥饿实验不能过长，否则结构物质会被分解，参数值会偏低。$[{E_m}]$值可以直接通过比较饱食个体最初的能量和饥饿后但死亡之前能量含量得出，也可通过比较个体在冬季和生长旺盛季节能量的差异间接估计得出，但这种方法耗时长且所得值偏小。3个参数均与饥饿过程有关，因此，通过饥饿实验可以同时获得$[{E_G}]$、$[{E_m}]$和$[{\dot p_M}]$的值。本研究3个参数的获取就是采用饥饿实验的方法。

几乎所有贝类的生长都受温度的影响(王有基等, 2014)，因Arrhenius温度${T_A}$值是模型中很重要的一个参数。温度对生长、摄食、耗氧、排氨和吸收效率都有影响，因此，Arrhenius温度可以通过测定温度对生物这几项指标的影响获得(张继红等, 2016)。其中，温度对生物的生长、摄食和吸收效率的影响通常需要长时间观测；排氨值的测定往往不够准确，通常食物残渣与生物粪便不好收集，容易造成数据偏高或偏低；测定耗氧相对来说耗时短且准确率相对高，因此，较多研究者通过测定温度对耗氧的影响来确定Arrhenius温度的值。本研究即通过温度对耗氧率的影响获得鲍的Arrhenius温度的值。

目前已有多种双壳贝类DEB模型参数的报道，其中，形状系数主要在0.17~0.39范围内，如太平洋牡蛎(Crassostrea gigas)的δm值为0.175，紫贻贝(Mytilus edulis)为0.287，虾夷扇贝为0.32等(van der Veer et al, 2006)。本研究测得的皱纹盘鲍形状系数是0.43，比已报道的双壳贝类数值要大，这也许与皱纹盘鲍是单壳贝类，其软组织湿重与壳长的比值要高于双壳贝类。

贝类Arrhenius温度${T_A}$的数值差异较大，一般品种贝类Arrhenius温度数值主要在4000~11000范围内，例如虾夷扇贝的${T_A}$值为4160(张继红等, 2016)；新西兰绿唇贻贝(Perna canaliculus)的${T_A}$值为5530 (Ren et al, 2005)；太平洋牡蛎幼虫的${T_A}$值为11000 (Rico-Villa et al, 2010)。本研究测得的鲍的${T_A}$值为7196，在已知研究报道的中上范围内。分析${T_A}$值差异较大的主要原因是不同地域、不同贝类种群对温度的响应适应能力有差异(常亚青, 2007)。

不同贝类饥饿实验相关参数值$[{E_G}]$、$[{\dot p_M}]$、$[{E_m}]$和${\mu _E}$值也有一定的差异，贝类$[{\dot p_M}]$和$[{E_m}]$的值在10~26和2000~3000范围内(van der Veer et al, 2006)。主要原因是不同贝类对饥饿胁迫的响应程度不同；同时，这几个参数都与体积有关，因此，单位体积的差距导致最终的参数值不同，例如虾夷扇贝(张继红等, 2016)在饥饿30 d后，软组织干重和耗氧率降低了56%和81%，而本研究测得皱纹盘鲍在饥饿35 d后，软组织干重和耗氧率较初始下降26%和70%，其中，耗氧率下降均在60%以上，这与贝类在饥饿后首先通过调节自身代谢水平来适应环境的变化，减少能量的消耗有关(何毛贤等, 2010; Mehner et al, 2010)；而软组织干重的下降率相差较大，这主要是因为皱纹盘鲍耐饥饿能力较强，一般体重下降12%~24%才开始死亡(Leighton et al, 1963)。

DEB模型中其他的参数，如温度函数中温度的上下限可根据鲍生长温度确定，结构物质体积根据鲍性腺发育成熟的壳长计算，吸收效率可根据已有研究得出。

DEB模型已广泛应用于双壳贝类，但对于鲍等单壳贝类研究较少。本研究通过实验计算了6个参数值，为进一步构建皱纹盘鲍DEB模型提供了必需的参数值，也为进一步研究其他单壳贝类提供了理论依据。