Kooijman (2000)在1986年首次提出了基于κ原则的动态能量收支(dynamic energy budget, DEB)理论，用于描述生物在个体层面上对于能量的吸收、储备和利用。它叙述的是生物将摄食同化能量的一部分用于维持身体结构的生长，另一部分用于性腺的发育和繁殖储备(Sousa et al, 2006; Ren et al, 2001)。基于DEB理论研究生物生理机制与环境关系而模拟出的个体生长模型称作动态能量收支模型，简称为DEB模型(Marinov et al, 2007; Kooijman, 2009)，该模型可在个体层面上预测特定物种的体长、体重和性腺等动态生长的变化(Bourlès et al, 2009; Bernard et al, 2011)。通过假设食物和温度是生物新陈代谢机制的主要驱动力，为理解生物的整体生理表现提供了一个全面的框架。DEB理论基于不同物种在新陈代谢上的一致性而具有非常广泛的应用范围，准确获得特定条件下的模型参数即能得到目标物种的DEB模型(张继红等, 2016)。DEB理论作为国内外的研究热点，已被成功地应用到鱼类(Ren et al, 2020)、贝类(Fuentes-Santos et al, 2019; 段娇阳等, 2020)、藻类(蔡碧莹等, 2019)等水生生物，构建起多种DEB模型。

凡纳滨对虾(Litopenaeus vannamei)原产于东太平洋暖水海域，系热带性虾类。作为世界上公认的优良养殖品种之一，因其具有耐低盐、耐高温、生长快、抗病力强等优点而深受人们的喜爱。凡纳滨对虾自1988年引入我国后便迅速发展并风靡全国，历经海湾养殖、池塘养殖和温棚养殖等几种养殖模式后，已成为我国重要的海水养殖品种(邓伟等, 2013)。如今，随着凡纳滨对虾养殖技术的成熟，全国各地掀起凡纳滨对虾养殖浪潮，尤其是工厂化高密度养殖成为凡纳滨对虾新的养殖模式(汪珂等, 2019)。但随着养殖规模和密度的扩大，种质退化、水质恶化和病害频发等一系列问题也随之浮现(姚晖, 2020)，因此，迫切需要养殖容量方面的理论指导。通过建立凡纳滨对虾动态能量收支模型并进一步建立其养殖容量模型，对于指导养殖管理和评估养殖容量具有重要意义(Sato et al, 2007; 刘慧等, 2018)。国外关于虾类DEB模型的研究已有多篇报道，建立了南极磷虾(Euphausia superba) (Jager et al, 2016)、褐虾(Brown shrimp) (Campos et al, 2009)和蓝虾(Litopenaeus stylirostris)等的DEB模型，但目前国内虾类DEB理论研究尚属空白，有待于进一步补充完善。

因此，本研究以工厂化高密度养殖的凡纳滨对虾为实验对象，参考国外已报道有关虾类DEB模型的研究方法，通过相关实验获得构建凡纳滨对虾DEB模型的5个必需参数，包括形状系数(shape coefficient, δm)、Arrhenius温度(arrhenius temperature, $ {T}_{A} $)、形成单位体积结构物质所需能量(volume-specific costs for structure, $ \text{ [}{E}_{G}\text{]} $)、单位体积最大储能(maximum storage density, $[{E_M}]$)和单位时间单位体积维持耗能率(volume-specific maintenance costs per unit of time, $[{\dot p_M}]$)。此项研究为后续凡纳滨对虾动态能量收支模型的构建奠定了基础，以期为凡纳滨对虾的工厂化高密度养殖容量和布局管理提供科学规划。

实验所用凡纳滨对虾均取自山东省海阳市黄海水产有限公司同一工厂化养虾车间。实验用虾经地笼捞出后迅速转移至实验桶内进行充气暂养，实验用桶容量为200 L，上口径为82 cm，下口径为68 cm，高度为53 cm，上覆黑色网布，防止对虾受刺激跳出。实验用水为天然海水，经沉淀、砂滤、调温、增氧处理后使用，水温为(28.0±0.5)℃，盐度为31，pH为7.8~8.2，溶氧保持在5 mg/L以上，与车间养殖环境保持一致。暂养期间，投喂青岛正大农业发展有限公司生产的凡纳滨对虾配合饲料，投喂时间分别为07:00、12:00、17:00和22:00。驯养至实验用虾成活率稳定后开始各个生理实验。

实验于2020年9月初至2021年1月中旬在海阳市黄海水产有限公司标准实验室进行。

凡纳滨对虾经中间培育后，每隔7 d从虾池随机捞取10尾虾直接用于形状系数测量，分别测定凡纳滨对虾的体长和湿重，共计78尾。体长用刻度尺(精度0.01 mm)测量，湿重用电子天平(龙蓓电子天平, I2000, 精度0.01 g)称量，湿重即为用卫生纸擦干体表水分，阴干0.5 h后的虾全重。根据湿重与虾体密度的乘积得到体积(V)。

式中，$V$为虾的体积(cm³)；δm为形状系数；$L$为虾的体长(cm)。

在凡纳滨对虾的不同生长阶段，选取经暂养后不同规格的3组[A组体长为：(5.04± 0.13) cm，B组：(7.09±0.18) cm，C组：(9.13±0.29) cm]用于测定不同实验温度对凡纳滨对虾单位干重耗氧率的影响。在22℃、26℃、30℃、34℃、38℃ 5个实验温度条件下，将3组不同规格的凡纳滨对虾设5组重复，3组空白对照。实验开始后在每个装满海水的密闭塑料瓶(1.5 L)中缓慢放入1尾虾，挤出多余气泡确保没有空气。塑料瓶置于水温为28℃的海水实验桶中，将水温逐步升温至30℃、34℃、38℃或自然降温至22℃、26℃，进行各个不同温度梯度的耗氧实验。凡纳滨对虾在升温或降温过程中调节自身代谢以逐渐适应环境变化，达到所需温度后在加热棒的维持下完成耗氧实验。耗氧时间持续1 h，利用便携式溶氧仪(希玛, AR8010+)测定实验前后密闭塑料瓶中的溶解氧(DO)浓度。耗氧实验结束后，测定每尾虾的干重，干重为在60℃电热恒温鼓风干燥箱(尚诚, 101-2B)中烘干72 h至无水分的重量。根据实验前后DO的浓度变化计算单位干重呼吸耗氧率[${\text{OR}}$, mg/(g∙h)]：

式中，DO₀、DO_t为各组实验开始和结束时瓶中DO的含量(mg/L)，V_L为塑料瓶体积(L)，DW为虾干重(g)，${t_1}$为耗氧实验时间(h)。

用地笼捞取300尾虾，暂养后随机平均分配，置于4个水桶进行饥饿实验，将水温控制在凡纳滨对虾生长的最适温度(28℃)，连续24 h不间断充气以确保氧气充足。实验桶设计为微流水，进水口套紧纱布过滤海水中的杂藻。随着实验的进行，及时清理桶底的粪便和桶壁附着的污物并及时隔离病虾，清除死虾和虾壳。饥饿实验每隔5 d取8只凡纳滨对虾，测定其单位干重呼吸耗氧率，另取10只凡纳滨对虾，测定湿重、干重和有机物含量。有机物含量用灰分测定法测定，即将称过干重的虾放入坩埚，置于马弗炉(分体式SX2-2.5-10A)中，450℃灼烧4 h后称重。根据质量差，计算获得有机物含量。饥饿实验在实验用虾干重不再降低、呼吸耗氧率基本保持恒定时结束(约31 d)。

实验期间，虾干重随体内储存能量的消耗而逐渐降低。而当虾的储备能量完全耗尽时，虾的干重将不再随饥饿时间而变化，此时的重量即为虾的结构物质，由此计算形成单位体积结构物质所需能量$\left[ {{E_G}} \right]$：

式中，${W_t}$为实验结束时保持恒定的虾干重(g)，${C_t}$为实验结束时虾的有机物含量(%)，$k$为有机物的能值(8000 J/g)，${T_r}$为生长效率的转换系数(${T_r}$=40%) (van der Veer et al, 2006)，$V$为虾体积(cm³)。

虾初始能量与饥饿后的结构物质能量之差即为虾的最大储能$[{E_M}]$：

式中，${W_0}$为虾干重的初始值(g)，${C_0}$为实验初始时虾有机物含量(%)。

由虾不随饥饿时间变化的呼吸耗氧率计算单位时间单位体积维持耗能率$[{\dot p_M}]$：

式中，OR为虾饥饿后基本恒定的单位干重呼吸耗氧率[mg/(ind.∙h)]，${E_o}$为O₂的能值(1 mL O₂=20.3 J) (Ren et al, 2008)，$t$为时间转化系数(1 d=24 h)，${\rho _o}$为O₂在28℃下的密度(1.295 mg/mL)。

实验数据采用Excel 2010进行统计分析与回归并作图；采用SPSS 25.0软件进行数据处理获取标准差，最终结果以平均值±标准差(Mean±SD)表示。

通过Excel 2010软件进行凡纳滨对虾体长与体积的拟合回归，结果符合三次函数(图 1)：V=0.009 3L^{3.109 4} (R²=0.998 7)，根据公式(1)将体长与体积的立方根进行线性回归，所得斜率(图 1)即为形状系数δm的值(0.23)。

图 1(Fig. 1)

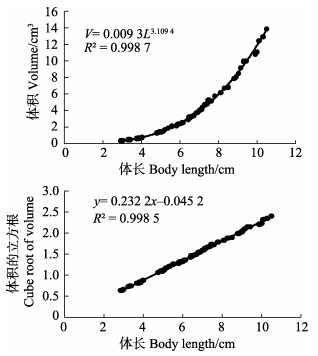
图 1 凡纳滨对虾体长与湿重的关系 Fig.1 Relationship between wet weight and body length of L. vannamei

统计作图后得到3组凡纳滨对虾(表 1)的单位干重耗氧率随个体规格的增大而减小(图 2)，随实验温度的上升呈先增大后减小的变化趋势。在22℃~34℃实验温度范围内，单位干重耗氧率随温度的升高而增大，在34℃达到最大；之后随温度的升高而减小。在34℃拐点前，根据3组凡纳滨对虾单位干重耗氧率的ln值与温度T (热力学温度，K)的倒数进行线性回归得到3组方程，分别为lnR=–6 470.6T^–1+22.118 (R²=0.963 3)、lnR=–5 770.9T^–1+19.502 (R²=0.952 8)、lnR=–6 230.5T^–1+20.849 (R²=0.977 3) (图 3)。3组方程斜率绝对值的平均值为6157 K，即凡纳滨对虾的${T_A}$值。

表 1(Tab.1)

表 1 3组凡纳滨对虾生物学特征 Tab.1 Biological characteristics of three groups of L. vannamei 指标Indices 组别Group A B C 体长Shell length/cm 5.04±0.13 7.09±0.18 9.13±0.29 湿重Wet weight/g 1.45±0.10 3.85±0.15 8.74±0.19 干重Dry weight/g 0.29±0.07 1.02±0.11 2.43±0.15

表 1 3组凡纳滨对虾生物学特征 Tab.1 Biological characteristics of three groups of L. vannamei

图 1(Fig. 1)

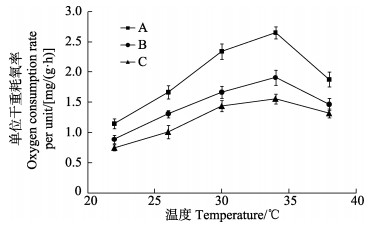
图 2 3组不同规格凡纳滨对虾在 Fig.2 Oxygen consumption rate per unit dry weight of three groups of different sizes of L. vannamei at different temperatures 不同温度下的单位干重耗氧率

图 1(Fig. 1)

图 3 凡纳滨对虾单位干重耗氧率的ln值与温度的倒数线性关系 Fig.3 Linear relationship between the ln value of the oxygen consumption rate per unit dry weight of L. vannamei and the reciprocal temperature

饥饿实验共进行31 d，实验所用凡纳滨对虾初始平均体长为(8.97±0.35) cm、平均体重为(8.87±0.22) g，实验期间凡纳滨对虾无能量摄入。随着实验时间的推移，凡纳滨对虾的干重不断下降并在第26天趋于恒定，测得对虾干重由(2.36±0.89) g降至(1.23±0.22) g (图 4)；呼吸耗氧率由最初的0.95 mg/(ind.∙h)逐渐下降，并在第31天左右稳定在0.58 mg/(ind.∙h)(图 5)。对虾干重和呼吸耗氧率的降幅分别为47.9%和38.9%，有机物含量则从82%降至62%(表 2)。

图 1(Fig. 1)

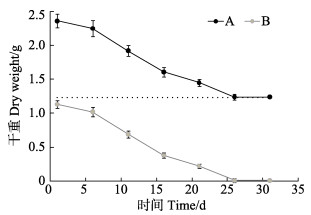
图 4 凡纳滨对虾干重(A)和存储物质(B)随饥饿时间的变化 Fig.4 Changes of dry weight (A) and storage of reserves (B) in L. vannamei during starvation

图 1(Fig. 1)

图 5 凡纳滨对虾耗氧率随饥饿时间的变化 Fig.5 Changes of oxygen consumption rate of L. vannamei at different starvation time

表 2(Tab.2)

表 2 饥饿实验相关参数计算值 Tab.2 Parameter calculated value related to the starvation experiment 参数Parameter 初始值Initial value 终末值Final value 结果Result 干重Dry weight/g 2.35±0.29 1.23±0.12 有机物含量Organic content/% 82.00±4.25 62.00±2.76 形成单位体积结构物质所需能量$[{E_G}]$/(J/cm3) 5826±258 单位体积最大储能$[{E_M}]$/(J/cm3) 2211±112 单位时间单位体积维持耗能率$[{\dot p_M}]$/[J/(cm3∙d)] 31.47±3.54

表 2 饥饿实验相关参数计算值 Tab.2 Parameter calculated value related to the starvation experiment

根据凡纳滨对虾饥饿实验结束后基本恒定的干重和有机物含量，利用公式(3)计算形成单位体积结构物质所需能量$\left[ {{E_G}} \right]$的值，为5826 J/cm³(表 2)；利用公式(4)计算单位体积最大存储能量$[{E_M}]$的值，为2211 J/cm³(表 2)。根据对虾不随饥饿时间变化而保持稳定的呼吸耗氧率，利用公式(5)计算单位时间单位体积维持耗能率$[{\dot p_M}]$的值，为31.47 J/(cm³∙d)(表 2)。

尽管DEB模型所需参数的数量较少，但参数的获取相对复杂，对参数精准度要求较高(Ren et al, 2008)。体积是DEB模型输出体长、干重等变量的关键因素且较难测量，综合考量本研究通过对虾湿重与密度的乘积获得(Sablani et al, 2004)。而形状系数δm是表征体积的重要参数，通过对虾湿重的立方根和体长进行线性回归得出。在目前已有虾类DEB模型参数的报道中，形状系数取值范围主要为0.2~0.3，如南极磷虾(Jager et al, 2016)的δm值为0.21，褐虾(Campos et al, 2009)为0.21，蓝虾为0.28等。但Mehner等(1994)研究显示，绿虎虾(Penaeus semisulcatus)的δm值为0.81，主要是因为其湿重与体长的比值远高于其他虾类。本研究为使形状系数更加准确有效，选取的样本覆盖整个生长过程，最终测得凡纳滨对虾的形状系数δm值为0.23，与大多数报道相近。

水温不仅是构建海洋物种DEB模型的重要强制函数，而且对凡纳滨对虾的能量收支也有重要意义。因为虾的摄食、生长、排氨、耗氧和同化等生理活动在很大程度上都受制于温度，所以模型参数中的Arrhenius温度$ {T}_{A}\text{ } $值可通过测定温度对生物这几项指标的影响获得(张继红等, 2017)。在实验室中，进行摄食、生长和同化实验需要的周期过长且繁琐，排氨实验由于虾粪便、饲料残渣的溶失和不易收集导致结果不准确。而耗氧实验往往实验周期短且结果精准(陈琴等, 2001)，因此本研究选择耗氧方案来获得凡纳滨对虾Arrhenius温度${T_A}$值。大多数虾类${T_A}$值主要在5500~9000范围内，例如南极磷虾(Jager et al, 2016)为5630，蓝虾为8000，褐虾(Campos et al, 2009)为9000。本研究测得凡纳滨对虾的${T_A}$值为6156，位于已知研究报道范围内。常亚青(2007)研究分析$ {T}_{A}\text{ } $值差异较大的主要原因是不同地域、不同种群对温度的响应适应能力有差异。水温在DEB模型中的赋值比较模糊，一般都是参考当地的水文条件，但天然水域的水温不仅随季节时间变化且随深度变化(Campos et al, 2009)。凡纳滨对虾的生活习性是昼伏夜出，昼夜所待的水层温度不一。Saborowski等(2000)研究表明，南极磷虾每天要接受6 h的表层水温和18 h的深层水温。而本研究中的工厂化养虾车间配有专业的供暖设备，使水温维持在27℃~28℃，水温不随时间和深度变化，因此本研究的$ {T}_{A}\text{ } $值比传统天然大水面模型更准确有效。

$\left[ {{E_G}} \right]$、$[{E_M}]$和$[{\dot p_M}]$是构建凡纳滨对虾DEB模型必需的3个参数，本研究参考van der Veer等(2006)测取双壳贝类的方法，通过饥饿实验获取数据转化求得这3个参数。根据凡纳滨对虾饥饿实验结束后的干重来计算$\left[ {{E_G}} \right]$的值，但饥饿时间不能过长，否则会造成结构物质分解以致参数值偏低；根据凡纳滨对虾初始和饥饿后的能量之差计算$[{E_M}]$值，Kooijman (2000)研究指出，可通过比较个体在生长旺盛季节和在冬季的能量之差间接估计得出，但这种方法周期过长且所得参数值偏低；根据凡纳滨对虾饥饿后基本恒定的呼吸耗氧率来计算$[{\dot p_M}]$的值。不同虾类的$\left[ {{E_G}} \right]$、$[{E_M}]$和$[{\dot p_M}]$值都有一定差异，其主要原因是不同虾类对饥饿胁迫的响应程度不同，导致最终的参数值不同。Kooijman (2000)研究表明，物种维持和生长所用能量的比例、单位结构体积的生长成本和最大储存密度与温度无关，并将在物种分布区保持不变。虾类$\left[ {{E_G}} \right]$和$[{E_M}]$的值一般分别在2500~6000和800~3000范围内，本研究得到的$\left[ {{E_G}} \right]$和$[{E_M}]$均在此范围内。Campos等(2009)研究将褐虾饥饿24 d后，发现干重和耗氧率分别降低了54%和45%，而本研究测得凡纳滨对虾在饥饿31 d后干重和耗氧率较初始值分别下降47.8%和38%。其中，耗氧率下降是因为在食物密度和储备能量变低时，对虾会通过调节自身代谢水平来适应环境的变化，减少能量的消耗(Mehner et al, 1994)。van der Veer等(2006)研究发现，虾类$[{\dot p_M}]$的值一般在15~60范围内，差异主要与不同虾类的单位体积大小密切相关，本研究获得的$[{\dot p_M}]$在此范围内。

目前，关于虾类DEB模型参数的报道较少，一个重要的因素是甲壳类物种的体长不是持续增加，而是通过周期性蜕壳完成的，而以往大都假设建模物种的各个尺寸指标是持续增长的。蜕去的虾壳也意味着同化的一部分能量流失，王吉桥等(2004)研究指出，这部分能量在3%左右，这也是模型模拟出的体长、干重比实测值偏小的原因之一。在以后的研究中，需要对虾类的蜕壳机制进行细致的探究来解决这一问题，Talbot等(2019)进行过甲壳类物种蜕壳的探索性研究。为解释清楚这一点，研究人员将DEB模型扩展到跟踪碳质量的持续增加以及物理尺寸的间歇性增加，为下一步研究指明了方向。本研究凡纳滨对虾的DEB建模研究中，整体生长仍被假设为连续的。

本研究得到的5个模型参数精准度虽有待提高，但都是有效的。在最优食物、水温条件下构建的凡纳滨对虾DEB模型是成功的，更加细致地模拟了凡纳滨对虾生长对环境的反馈。DEB模型作为国内外研究热点已广泛应用于多种海洋生物，但对于对虾等甲壳类研究较少。本研究通过相关实验获得了构建凡纳滨对虾动态能量收支模型的5个必需参数，为后续凡纳滨对虾动态能量收支模型的构建奠定了基础，也为进一步研究其他甲壳类动物提供了理论依据，以期为凡纳滨对虾的工厂化高密度养殖提供理论支撑。